题目内容
【题目】质量为m的物体用轻绳AB悬挂于天花板上.用水平向左的力F缓慢拉动绳的中点O,如图所示.用T表示绳OA段拉力的大小,在O点向左移动的过程中( )
A.F逐渐变大,T逐渐变大
B.F逐渐变大,T逐渐变小
C.F逐渐变小,T逐渐变大
D.F逐渐变小,T逐渐变小
【答案】A
【解析】解:以结点O为研究对象受力分析如下图所示:
由题意知点O缓慢移动,即在移动过程中始终处于平衡状态,则可知:
绳OB的张力TB=mg
根据平衡条件可知:
Tcosθ﹣TB=0
Tsinθ﹣F=0
由此两式可得:
F=TBtanθ=mgtanθ
T= ![]()
在结点为O被缓慢拉动过程中,夹角θ增大,由三角函数可知:
F和T均变大,故A正确,BCD错误.
故选:A.
本题关键是抓住悬挂物B的重力不变,即OB段绳中张力恒定,O点缓慢移动时,点O始终处于平衡状态,根据平衡条件列式求解各力变化情况.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
【题目】某同学在竖直悬挂的轻质弹簧下加挂钩码,探究弹力与弹簧伸长量的关系.下表是该同学的实验数据.实验时弹簧始终未超过弹性限度.
砝码质量m×10﹣3kg | 0 | 30 | 60 | 90 | 120 | 150 |
弹簧总长度l×10﹣2m | 6.0 | 7.2 | 8.4 | 9.6 | 10.8 | 12.0 |
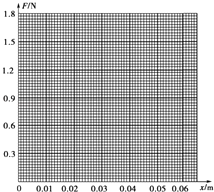
(1)根据实验数据在坐标系中作出弹力F跟弹簧伸长量x关系的图象.(不考虑弹簧自身重力)
(2)根据图象得到弹簧的劲度系数是 N/m.(结果保留两位有效数字)


