题目内容
17.某兴趣小组利用沙摆(视为单摆)测量斜面上木板运动的加速度,实验装置如图甲.
(1)测量沙摆周期时,为减小误差,应取沙摆运动到最低点(填“最高点”或“最低点”)时作为计时起点
(2)某同学用秒表计下n次全振动的时间如图乙所示,示数为70.3s;
(3)在沙摆振动时,将一木板从斜面上滑下,沙摆漏下的沙木板上形成如图丙所示形状.测得沙摆周期为T,AB=s1,BC=s2,则木板加速度a=$\frac{4({s}_{2}-{s}_{1})}{{T}^{2}}$(用s1,s2,T表示).
分析 测单摆周期时,为准确计时、减小实验误差,从单摆经过最低点时开始计时;秒表分针与秒针示数之和是秒表示数;应用匀变速直线运动的推论:△x=at2可以求出加速度.
解答 解:(1)测量沙摆周期时,为减小误差,应取沙摆运动到最低点时作为计时起点;
(2)由图乙所示秒表可知,秒表示数为60s+10.3s=70.3s;
(3)由图丙所示可知,A到B、C到D的时间间隔都相等,为:t=$\frac{1}{2}T$,
木板做匀加速直线运动,由匀变速直线运动的推论:△x=at2可知,
木板的加速度:a=$\frac{{s}_{2}-{s}_{1}}{(\frac{T}{2})^{2}}$=$\frac{4({s}_{2}-{s}_{1})}{{T}^{2}}$.
故答案为:(1)最低点;(2)70.3;(3)$\frac{4({s}_{2}-{s}_{1})}{{T}^{2}}$.
点评 解决本题的关键知道实验的原理,掌握秒表的读数方法,对于第三问,结合匀变速直线运动的推论进行求解,注意相等的时间为$\frac{1}{2}T$.难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列关于速度和加速度的说法中正确的是( )
| A. | 物体加速度增大,速度就增大 | |
| B. | 物体速度变化得越快,速度就越大 | |
| C. | 物体速度越大,速度的变化率就越大 | |
| D. | 物体运动快慢和运动速度变化快慢不是一样的 |
8. 电源、开关S、定值电阻R1、光敏电阻R2和电容器连成如图所示电路,电容器的两平行板水平放置,当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点,当用强光照射光敏电阻R2时,光敏电阻R2的阻值变小,则( )
电源、开关S、定值电阻R1、光敏电阻R2和电容器连成如图所示电路,电容器的两平行板水平放置,当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点,当用强光照射光敏电阻R2时,光敏电阻R2的阻值变小,则( )
 电源、开关S、定值电阻R1、光敏电阻R2和电容器连成如图所示电路,电容器的两平行板水平放置,当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点,当用强光照射光敏电阻R2时,光敏电阻R2的阻值变小,则( )
电源、开关S、定值电阻R1、光敏电阻R2和电容器连成如图所示电路,电容器的两平行板水平放置,当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点,当用强光照射光敏电阻R2时,光敏电阻R2的阻值变小,则( )| A. | 液滴带正电 | B. | 液滴向上运动 | ||
| C. | 电容器所带电荷量减少 | D. | 电容器两极板间电压变大 |
5.关于质点作匀速圆周运动的下列说法,正确的是( )
| A. | 线速度v与角速度ω不变 | B. | 质点的动能Ek一定不变 | ||
| C. | 合外力F合与加速度a不变 | D. | 质点的机械能E一定不变 |
12.质量为m的小球做平抛运动,已知重力加速度为g,根据下列哪个条件可求出小球初速度( )
| A. | 水平位移 | B. | 下落高度 | ||
| C. | 落地时的动能 | D. | 落地时的速度大小和方向 |
2.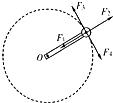 如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
 如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )| A. | 沿F2的方向 | B. | 沿F1的方向 | C. | 沿F3的方向 | D. | 沿F4的方向 |
6.对于红、绿、蓝三种单色光,下列表述正确的是( )
| A. | 红光频率最高 | B. | 蓝光频率最高 | ||
| C. | 绿光光子能量最小 | D. | 蓝光光子能量最小 |
7. 如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )
如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )
 如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )
如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )| A. | 质点从M到N过程中速度大小保持不变 | |
| B. | 质点在这两段时间内的速度变化量大小相等,方向相同 | |
| C. | 质点在这两段时间内的速度变化量大小不相等,方向相同 | |
| D. | 质点在MN间的运动是加速运动 |
