Question

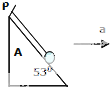如图所示，小球的质量为m，斜面光滑，小球与斜面向右匀加速运动，求：
（1）为保持小球与斜面体相对静止，问斜面体的最大加速度不能超过多少？
（2）当a=

g

2

时，求绳子的张力多大？

Answer 1

分析：（1）当绳子为零时，斜面体的加速度最大，抓住小球和斜面体加速度相同，隔离对小球分析，运用牛顿第二定律求出加速度的大小．
（2）对小球受力分析，根据竖直方向上合力为零，水平方向上合力产生加速度，根据牛顿第二定律求出绳子的张力大小．

解答：解：（1）当绳子的拉力为零时，斜面体的加速度最大．
对小球，根据牛顿第二定律得，mgtan53°=ma
解得a=gtan53°=

4

3

g．
（2）当a=

g

2

时，根据牛顿第二定律，运用正交分解得，
Tcos37°+Ncos53°=mg．
Nsin53°-Tsin37°=ma
代入数据，联立解得T=

25

34

mg．
答：（1）为保持小球与斜面体相对静止，斜面体的最大加速度不能超过

4

3

g．
（2）当a=

g

2

时，绳子的张力为

25

34

mg．

点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解，知道加速度最大时的临界情况．