题目内容
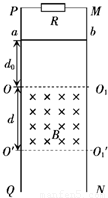
如图所示,竖直放置的光滑平行金属导轨MN、PQ相距L,在M点和P点间接有一个阻值为R的电阻,在两导轨间的矩形区域OO1O1′O′内有垂直导轨平面向里、宽为d的匀强磁场,磁感应强度为B.一质量为m、电阻为r的导体棒ab垂直地搁在导轨上,与磁场的上边界相距d.现使ab棒由静止开始释放,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好接触且下落过程中始终保持水平,导轨的电阻不计).(1)求棒ab离开磁场的下边界时的速度大小.
(2)求棒ab进入磁场区域匀速运动前速度达到v1时的加速度大小.
(3)求棒ab在通过磁场区的过程中产生的焦耳热.
【答案】分析:(1)棒ab在离开磁场做匀速直线运动,重力与安培力平衡,由E=BLv、I=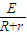 、F=BIL推导出安培力,由平衡条件求出棒ab离开磁场的下边界时的速度大小.
、F=BIL推导出安培力,由平衡条件求出棒ab离开磁场的下边界时的速度大小.
(2)推导安培力的表达式得到速度达到v1时的安培力大小,根据牛顿第二定律求出加速度.
(3)棒ab从静止释放到刚出磁场的过程,根据能量守恒定律求解在通过磁场区的过程中回路产生的焦耳热,由焦耳定律求解棒ab在通过磁场区的过程中产生的焦耳热.
解答: 解:(1)设棒ab离开磁场的边界前做匀速运动的速度为v,产生的感应电动势为:E=BLv …①
解:(1)设棒ab离开磁场的边界前做匀速运动的速度为v,产生的感应电动势为:E=BLv …①
电路中的电流I=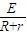 …②
…②
对棒ab,由平衡条件得:mg-BIL=0 …③
联立①②③解得:v=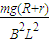 …④
…④
(2)设棒ab进入磁场区域匀速运动前速度达到v1时的加速度大小为a,则:
产生的感应电动势为:E1=BLv1…⑤
电路中的电流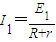 …⑥
…⑥
则由牛顿第二定律可得:mg-BIL=ma…⑦
联立①②⑤解得: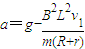 …⑧
…⑧
(3)设整个回路中产生的焦耳热为Q,由能量的转化和守恒定律可得:
mg(d+d)=Q+ mv2 …⑨
mv2 …⑨
联立④⑤解得:Q=mg(d+d)-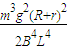 …⑩
…⑩
由于通过棒ab和电阻R的电流始终相等,由焦耳定律可得,棒ab在通过磁场区的过程中产生的焦耳热Qab为:
Qab=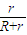 [mg(d+d)-
[mg(d+d)-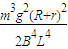 ]
]
答:
(1)棒ab离开磁场的下边界时的速度大小是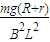 .
.
(2)求棒ab进入磁场区域匀速运动前速度达到v1时的加速度大小是g.
(3)求棒ab在通过磁场区的过程中产生的焦耳热是Qab=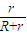 [mg(d+d)-
[mg(d+d)-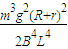 ].
].
点评:本题是电磁感应与力学知识的综合,关键由E=BLv、I=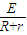 、F=BIL推导出安培力.
、F=BIL推导出安培力.
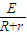 、F=BIL推导出安培力,由平衡条件求出棒ab离开磁场的下边界时的速度大小.
、F=BIL推导出安培力,由平衡条件求出棒ab离开磁场的下边界时的速度大小.(2)推导安培力的表达式得到速度达到v1时的安培力大小,根据牛顿第二定律求出加速度.
(3)棒ab从静止释放到刚出磁场的过程,根据能量守恒定律求解在通过磁场区的过程中回路产生的焦耳热,由焦耳定律求解棒ab在通过磁场区的过程中产生的焦耳热.
解答:
 解:(1)设棒ab离开磁场的边界前做匀速运动的速度为v,产生的感应电动势为:E=BLv …①
解:(1)设棒ab离开磁场的边界前做匀速运动的速度为v,产生的感应电动势为:E=BLv …①电路中的电流I=
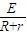 …②
…②对棒ab,由平衡条件得:mg-BIL=0 …③
联立①②③解得:v=
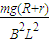 …④
…④(2)设棒ab进入磁场区域匀速运动前速度达到v1时的加速度大小为a,则:
产生的感应电动势为:E1=BLv1…⑤
电路中的电流
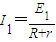 …⑥
…⑥则由牛顿第二定律可得:mg-BIL=ma…⑦
联立①②⑤解得:
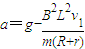 …⑧
…⑧(3)设整个回路中产生的焦耳热为Q,由能量的转化和守恒定律可得:
mg(d+d)=Q+
 mv2 …⑨
mv2 …⑨联立④⑤解得:Q=mg(d+d)-
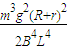 …⑩
…⑩由于通过棒ab和电阻R的电流始终相等,由焦耳定律可得,棒ab在通过磁场区的过程中产生的焦耳热Qab为:
Qab=
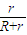 [mg(d+d)-
[mg(d+d)-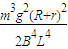 ]
]答:
(1)棒ab离开磁场的下边界时的速度大小是
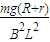 .
.(2)求棒ab进入磁场区域匀速运动前速度达到v1时的加速度大小是g.
(3)求棒ab在通过磁场区的过程中产生的焦耳热是Qab=
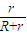 [mg(d+d)-
[mg(d+d)-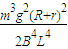 ].
].点评:本题是电磁感应与力学知识的综合,关键由E=BLv、I=
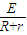 、F=BIL推导出安培力.
、F=BIL推导出安培力. 
练习册系列答案
相关题目
 如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为
如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为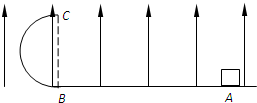 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小 如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )
如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( ) 物理选修3-3
物理选修3-3 如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求
如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求