题目内容
如图所示，竖直直角坐标系，第一象限有水平向左的匀强电场E1，第四象限有垂直于纸面向外的匀强磁场，且直线Y=—L下方处有竖直向下的匀强电场E2.质量为m的小球自A(0，L/2)处以v0的初速度水平抛出，小球到达B(L,0)处是速度方向恰好与x轴垂直．在B处有一内表面粗糙的圆筒，筒内壁与小球间的动摩擦因数为μ，筒直径略大于小球直径，筒长为L，竖直放置．已
知小球在离开筒以前就已经匀速，且离开筒后做匀速圆周运动，恰在D(0，-2L)处水平进入第三象限．求：
（1）E1∶E2是多少？
（2）在圆筒内摩擦力做功是多少？
解：（1）（8分）在第一象限，水平方向小球做匀减速运动，
加速度大小为：a＝
（1分）
由运动学公式，有：L＝
at2 （1分）
竖直方向做自由落体运动，有：
＝gt2 （1分）
由①②得，a＝2g （1分）
由牛顿第二定律可知，qE1＝2mg （1分）
小球在第四象限的电磁场中做匀速圆周运动，应有电场力与重力平衡，即：
qE2＝mg （2分）
故：E1∶E2＝2∶1. （1分）
（2）（11分）设小球进入圆筒时的速度为v1，在第一象限，由运动规律有：
竖直方向：＝
t （1分） 水平方向：L＝
t （1分）
解得：v1＝ （1分）
小球在圆筒中做加速度减小的加速运动，当重力与摩擦力相等时，开始做匀速运动，设此速度为v2，由平衡条件，有：mg＝μBqv2 （1分） 解得：v2＝
（1分）
在第四象限的电磁场中做匀速圆周运动时，
洛伦兹力提供向心力，有：Bqv2＝m
（2分） 解得，v2＝ 
（1分）
从小球进入圆筒到离开圆筒，由动能定理，有： mgL+Wf＝mv
－mv
（2分）
解之得：Wf＝－[mgL(1－
)＋
mv
] （2分）
在地面上方某处的真空室里存在着水平方向的匀强电场，以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系．一质量为m、带电荷量为+q的微粒从点P（l，0）由静止释放后沿直线PQ运动．当微粒到达点Q（0，-l）的瞬间，突然将电场方向顺时针旋转90°，同时加上一个垂直于纸面向外的匀强磁场（图中未画出），磁感应强度的大小B=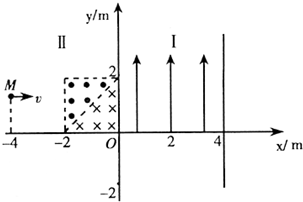
如图所示，在直角坐标系的第Ⅰ象限0≤x≤4区域内，分布着场强为E=
在地面上方某处的真空室里存在着水平方向的匀强电场，以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系．一质量为m、带电荷量为+q的微粒从点P（