题目内容
如图所示，在真空中半径为R=
m的圆形磁场区域里加上垂直于纸面向外的磁感应强度为B1=1T的匀强磁场，在圆形磁场区域外加上与B1方向相反的匀强磁场B2，P、Q是圆周上过直径的两个点，从P点沿半径方向以v =1×104m/s射入一质量m=5×10 -10kg，电荷量q=+5×10-6C的带电粒子，不计重力作用。
求：（1）若要使该粒子从P出发，经B1、B2磁场，第一次从Q点沿半径方向射入圆形磁场区域，则所需磁场B2的大小。（2）粒子从P点射入后第一次回到P点经过的时间。
带电粒子在圆形磁场中做圆周运动的半径为r1，圆心为O1
（1）
（2分）
1m （2分）
tan∠POO1=
∠POO1=30º （2分）
粒子从M点离开圆形磁场后，在B2磁场中中做圆周运动的半径为r2，圆心为O2 ，
由几何关系得：∠MOO2=60º （2分）
r2=Rtan60º=3m （1分）
T （1分）
（2）
（2分）
t1=
=
×10-4s （1分）
=6π×10-4s （2分）
t2=
=5π×10-4s （1分）
粒子由Q点进入圆形磁场后，有对称性可知，粒子第一次回到P点经过的时间
=
×10-4s （2分）
 |
练习册系列答案
发散思维新课堂系列答案
相关题目
半圆柱形玻璃砖的圆心在O点，一束红光和一束紫光从不同角度对准O点射向玻璃砖，如图所示．结果两种色光都沿OC方向射出，则（ ）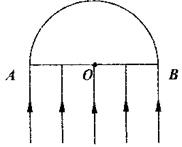
单色平行光a垂直射向一半径为R的玻璃半球的平面，其截面如图所示，发现半圆弧ACB上只有
区域有光射出（不考虑光反射后）的折射光线．若将单色平行光a换成单色平行光b，发现半圆弧ACB上只有
区域有光射出（同样不考虑光反射后的折射光线）．则下列说法正确的是（ ）