题目内容
小球沿光滑的斜轨道由静止开始滑下，并进入在竖直平面内的离心轨道运动，如图所示，为保持小球能够通过离心轨道最高点而不落下来，求小球至少应从多高处开始滑下？已知离心圆轨道半径为R，不计各处摩擦．
【答案】分析：使小球能够通过圆轨道最高点，那么小球在最高点时应该是恰好是物体的重力作为物体的向心力，由向心力的公式可以求得此时的最小的速度，再由机械能守恒可以求得离地面的高度h．
解答：解：取离心轨道最低点所在平面为参考平面，根据机械能守恒定律，有：
①
小球能够通过离心轨道最高点，应满足：
②
由以上两式解得：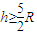
．
答：要使小球能通过圆形轨道的最高点，h至少应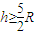
．
点评：本题属于圆周运动中绳的模型，在最高点时应该是重力恰好做为圆周运动的向心力，对于圆周运动中的两种模型一定要牢牢的掌握住．
解答：解：取离心轨道最低点所在平面为参考平面，根据机械能守恒定律，有：
①小球能够通过离心轨道最高点，应满足：
②由以上两式解得：
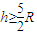．答：要使小球能通过圆形轨道的最高点，h至少应
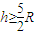．点评：本题属于圆周运动中绳的模型，在最高点时应该是重力恰好做为圆周运动的向心力，对于圆周运动中的两种模型一定要牢牢的掌握住．
练习册系列答案
相关题目
小球沿光滑的斜轨道由静止开始滑下，并进入在竖直平面内的离心轨道运动，如图所示，为保持小球能够通过离心轨道最高点而不落下来，求小球至少应从多高处开始滑下？已知离心圆轨道半径为R，不计各处摩擦．
