题目内容
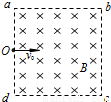
如图所示,在一个正方形区域abcd内存在磁感应强度为B、方向垂直纸面向里的匀强磁场,现从ad边的中心O点处,垂直磁场方向射入一速度为v的带正电粒子,v与ad边垂直.已知粒子质量为m,带电量为q,正方形的边长为L,不计粒子的重力.(1)若要使粒子能从ab边射出磁场,求v的大小范围;
(2)粒子在磁场中运动的最长时间是多少?
【答案】分析:(1)粒子进入磁场中.由洛伦兹力提供向心力,由牛顿第二定律得到半径公式r=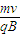 ,粒子的速度v越大,轨迹半径r越大.粒子从ab边射出磁场时,从a点射出,轨迹半径最小,对应的速度最小,从b点射出,轨迹半径最大,对应的速度最大,根据几何关系求出半径,再由牛顿第二定律求出对应的速度,即可得到速度的范围.
,粒子的速度v越大,轨迹半径r越大.粒子从ab边射出磁场时,从a点射出,轨迹半径最小,对应的速度最小,从b点射出,轨迹半径最大,对应的速度最大,根据几何关系求出半径,再由牛顿第二定律求出对应的速度,即可得到速度的范围.
(2)粒子在磁场中运动的周期T=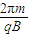 ,运动时间t=
,运动时间t=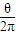 T,θ是轨迹所对应的圆心角,T是一定的,θ越大,t越大,当θ最大时,t最长.由图知,θ最大为π,则知最长时间为
T,θ是轨迹所对应的圆心角,T是一定的,θ越大,t越大,当θ最大时,t最长.由图知,θ最大为π,则知最长时间为 T.
T.
解答:解:(1)当粒子从a点射出时,轨迹半径最小,设为r1.对应的速度最小,设为v1.当粒子从从b点射出时,轨迹半径最大,设为r2.对应的速度最大,设为v2.
根据几何关系得:r1= L,
L,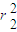 =L2+
=L2+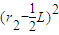
则得 r2=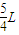
根据牛顿第二定律得:qvB=m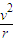
则得v=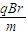
故有v1=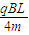 ,v2=
,v2=
所以要使粒子能从ab边射出磁场,v的大小范围为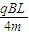 ≤v≤,5qBL4m
≤v≤,5qBL4m
(2)粒子运动周期为 T=
当粒子从oa边射出时,转过的圆心角最大,为π.故粒子在磁场中运动的最长时间为t= T=
T=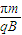 .
.
答:
(1)要使粒子能从ab边射出磁场,v的大小范围为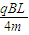 ≤v≤
≤v≤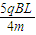 .
.
(2)粒子在磁场中运动的最长时间为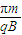 .
.
点评:带电粒子在磁场中运动的类型,确定向心力来源,画出轨迹,运用牛顿第二定律列式是惯用的解题思路.平时要加强训练,才能运用自如.
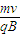 ,粒子的速度v越大,轨迹半径r越大.粒子从ab边射出磁场时,从a点射出,轨迹半径最小,对应的速度最小,从b点射出,轨迹半径最大,对应的速度最大,根据几何关系求出半径,再由牛顿第二定律求出对应的速度,即可得到速度的范围.
,粒子的速度v越大,轨迹半径r越大.粒子从ab边射出磁场时,从a点射出,轨迹半径最小,对应的速度最小,从b点射出,轨迹半径最大,对应的速度最大,根据几何关系求出半径,再由牛顿第二定律求出对应的速度,即可得到速度的范围.(2)粒子在磁场中运动的周期T=
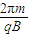 ,运动时间t=
,运动时间t=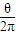 T,θ是轨迹所对应的圆心角,T是一定的,θ越大,t越大,当θ最大时,t最长.由图知,θ最大为π,则知最长时间为
T,θ是轨迹所对应的圆心角,T是一定的,θ越大,t越大,当θ最大时,t最长.由图知,θ最大为π,则知最长时间为 T.
T.解答:解:(1)当粒子从a点射出时,轨迹半径最小,设为r1.对应的速度最小,设为v1.当粒子从从b点射出时,轨迹半径最大,设为r2.对应的速度最大,设为v2.
根据几何关系得:r1=
 L,
L,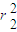 =L2+
=L2+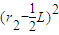
则得 r2=
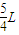
根据牛顿第二定律得:qvB=m
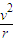
则得v=
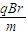
故有v1=
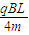 ,v2=
,v2=
所以要使粒子能从ab边射出磁场,v的大小范围为
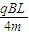 ≤v≤,5qBL4m
≤v≤,5qBL4m(2)粒子运动周期为 T=

当粒子从oa边射出时,转过的圆心角最大,为π.故粒子在磁场中运动的最长时间为t=
 T=
T=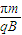 .
.答:
(1)要使粒子能从ab边射出磁场,v的大小范围为
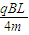 ≤v≤
≤v≤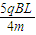 .
.(2)粒子在磁场中运动的最长时间为
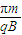 .
.点评:带电粒子在磁场中运动的类型,确定向心力来源,画出轨迹,运用牛顿第二定律列式是惯用的解题思路.平时要加强训练,才能运用自如.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图所示,在一个绝缘水平面上建立x轴,在过原点O垂直于x轴的虚线右侧有一个匀强电场,场强大小E=6.0×l05 N/C,方向与x轴正方向相同.在O点放一个电荷量q=-5.0xl0-8C、质量m=1.0×10 -2kg的带电物块.沿x轴正方向给物块一个初速度vo=2.0m/s使物块向右运动,物块与水平面间的动摩擦因数μ=0.20,g取10m/s2.求:
如图所示,在一个绝缘水平面上建立x轴,在过原点O垂直于x轴的虚线右侧有一个匀强电场,场强大小E=6.0×l05 N/C,方向与x轴正方向相同.在O点放一个电荷量q=-5.0xl0-8C、质量m=1.0×10 -2kg的带电物块.沿x轴正方向给物块一个初速度vo=2.0m/s使物块向右运动,物块与水平面间的动摩擦因数μ=0.20,g取10m/s2.求:
 如图所示,在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6.0×105N/C,方向与x轴正方向相同.在O处放一个电荷量-5.0×10-8C、质量m=1.0×10-2kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=4.0m/s,求物块最终停止时的位置.(g取10m/s2)
如图所示,在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6.0×105N/C,方向与x轴正方向相同.在O处放一个电荷量-5.0×10-8C、质量m=1.0×10-2kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=4.0m/s,求物块最终停止时的位置.(g取10m/s2)
