题目内容
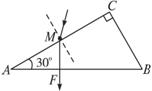
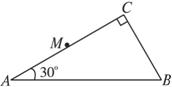
 如图所示,在以等边三角形abc为边界的区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B=1T,磁场方向垂直于abc平面向里.其中等边三角形边长L=2
如图所示,在以等边三角形abc为边界的区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B=1T,磁场方向垂直于abc平面向里.其中等边三角形边长L=2| 3 |
(1)求电场强度的大小和方向;
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经过t=0.5s恰好从区域的边界中点Q射出.求粒子比荷q/m的大小;
(3)若仅撤去电场,带电粒子仍从O点同方向射入,且恰好也从区域的边界另一中点P射出,求粒子速度v的大小.
分析:(1)带电粒子做匀速直线运动,处于平衡状态,所受合力为零,由平衡条件可以求出电场电动的大小与方向.
(2)撤去磁场粒子做类平抛运动,由类平抛运动知识可以求出粒子的比荷.
(3)带电粒子在磁场中做匀速圆周运动,由几何知识求出其轨道半径,由牛顿第二定律可以求出粒子的速度.
(2)撤去磁场粒子做类平抛运动,由类平抛运动知识可以求出粒子的比荷.
(3)带电粒子在磁场中做匀速圆周运动,由几何知识求出其轨道半径,由牛顿第二定律可以求出粒子的速度.
解答:解:(1)粒子由O至c做匀速直线运动,
由平衡条件得:qv0B=qE,
解得:E=v0B=3×1=3N/C,
由左手定则可知,洛伦兹力方向水平向左,
则电场力方向水平向右,粒子带正电,则E的方向:水平向右;
(2)O到Q的水平距离:x=
sin30°=
m,
仅撤去磁场后,带电粒子做类平抛运动,
由题意知,粒子运动时间:t=0.5s,
Ob方向上:x=
=
at2,
由牛顿第二定律得:qE=ma,
解得:
=
C/kg;
(3)仅撤去电场,带电粒子在磁场中匀速圆周运动.
粒子由中点P射出,由几何关系可知,粒子的轨道半径:R=
m,
由牛顿第二定律得:qvB=m
,
解得:v=
=4m/s;
答:(1)电场强度的大小为3N/C,方向水平向右;
(2)粒子比荷大小为
;
(3)粒子速度v的大小为4m/s.
由平衡条件得:qv0B=qE,
解得:E=v0B=3×1=3N/C,
由左手定则可知,洛伦兹力方向水平向左,
则电场力方向水平向右,粒子带正电,则E的方向:水平向右;
(2)O到Q的水平距离:x=
| L |
| 2 |
| ||
| 2 |
仅撤去磁场后,带电粒子做类平抛运动,
由题意知,粒子运动时间:t=0.5s,
Ob方向上:x=
| ||
| 2 |
| 1 |
| 2 |
由牛顿第二定律得:qE=ma,
解得:
| q |
| m |
4
| ||
| 3 |
(3)仅撤去电场,带电粒子在磁场中匀速圆周运动.
粒子由中点P射出,由几何关系可知,粒子的轨道半径:R=
| 3 |
由牛顿第二定律得:qvB=m
| v2 |
| R |
解得:v=
| qBR |
| m |
答:(1)电场强度的大小为3N/C,方向水平向右;
(2)粒子比荷大小为
4
| ||
| 3 |
(3)粒子速度v的大小为4m/s.
点评:本题考查了带电粒子在复合场、电场与磁场中的运动,应用平衡条件、类平抛运动、牛顿第二定律即可正确解题;解题时注意数学知识的应用.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 在直角坐标系xoy中有三个靠在一起的等大的圆形区域,分别存在着方向如图所示匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径
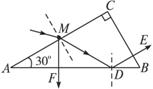
在直角坐标系xoy中有三个靠在一起的等大的圆形区域,分别存在着方向如图所示匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径 如图所示,边长为3L的等边三角形APC区域存在垂直于纸面向外的匀强磁场,磁感应强度大小为B.D、E、F三点分别在PC、CA、AP边上,AF=PD=CE=L.现有一质量为m、电荷量为q的带正电离子(不计重力),从F点以速度v向三角形内射人.
如图所示,边长为3L的等边三角形APC区域存在垂直于纸面向外的匀强磁场,磁感应强度大小为B.D、E、F三点分别在PC、CA、AP边上,AF=PD=CE=L.现有一质量为m、电荷量为q的带正电离子(不计重力),从F点以速度v向三角形内射人.