题目内容
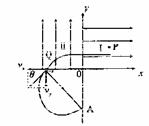
如图所示,在Oxy平面的第一象限和第二象限区域内,分别存在场强大小均为E的匀强
电场I和II,电场I的方向沿X轴正方向,电场II的方向沿Y轴的正方向。在第三象限
内存在垂直于Oxy平面的匀强磁场III,Q点的坐标为(-x0,0)。已知电子的电量为-e,
质量为m(不计电子所受重力)。
(1)在第一象限内适当位置由静止释放电子,电子经匀强电场I和II后恰能通过Q点。
求释放占的位置坐标x、y应满足的关系式;
(2)若要电子经匀强电场I和II后过Q点时动能最小,电子应从第一象限内的哪点由静止释放?求该点的位置和过Q点时的最小动能。
|
(1)设电子从第一象限内坐标为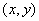 处由静止释放能过Q点,到达y轴时的速度为
处由静止释放能过Q点,到达y轴时的速度为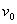 ,
,
由动能定理得: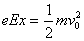 ① 1分
① 1分
若能到达Q,则应满足: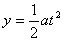 ② 1分
② 1分
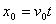 ③ 1分
③ 1分
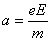 ④ 1分
④ 1分
联立①②③④得: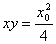 ⑤ 1分
⑤ 1分
(2)由动能定理得:电子从P由静止释放,经匀强电场I和II后过Q点时动能:
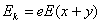 ⑥ 1分
⑥ 1分
而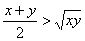 (当x=y时取“=”) ⑦ 1分
(当x=y时取“=”) ⑦ 1分
由⑤⑥⑦得: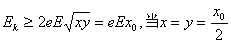 时取“=” ⑧1分
时取“=” ⑧1分
所以电子从第一象限内的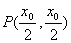 点由静止释放过Q点时动能最小,最小动能是
点由静止释放过Q点时动能最小,最小动能是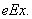
(3)若区域III中的匀强磁场方向垂直纸面向里,则电子左偏,不会再到达y轴,所以匀强磁场方向垂直纸面向外。运动轨迹如图,则:
|
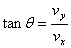
而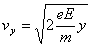
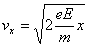
在满足条件(2)的情况下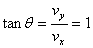 所以
所以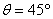 ⑨ 1分
⑨ 1分
设在区域III中做匀速圆周运动的半径为r,到达y轴上的A点,结合题中条件可推知,电子在幸亏中运动的轨迹应为以QA为直径的半圆,OA=x0,由几何知识知:
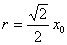 ⑩ 2分
⑩ 2分
设到达Q点的速度为v1,则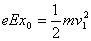 (11) 1分
(11) 1分
解得: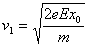 (12) 1分
(12) 1分
根据牛顿第二定律: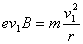 解得
解得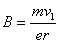 (13) 2分
(13) 2分
把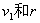 的值代入,第三象限内的匀强磁场的磁感应强度
的值代入,第三象限内的匀强磁场的磁感应强度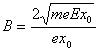
(14) 1分


 如图所示,在Oxy平面的ABCD区域内.存在一个边长为L的正方形匀强电场区域I,场强大小为E,方向沿z轴正方向;和一个边长也为L的正方形匀强磁场区域Ⅱ,磁感应强度为B=
如图所示,在Oxy平面的ABCD区域内.存在一个边长为L的正方形匀强电场区域I,场强大小为E,方向沿z轴正方向;和一个边长也为L的正方形匀强磁场区域Ⅱ,磁感应强度为B=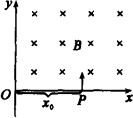

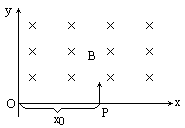
 ,方向垂直于纸面向外.m、e为电子的质量和电荷量(不计电子所受重力).现将电子在该区域AB边的中点处由静止释放.试求:
,方向垂直于纸面向外.m、e为电子的质量和电荷量(不计电子所受重力).现将电子在该区域AB边的中点处由静止释放.试求: