题目内容
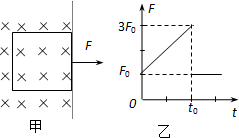 如图甲所示,一个正方形金属框位于有界匀强磁场区域内,线框的右边紧贴着边界,t=0时刻对线框施加一水平向右的外力F,让线框从静止开始做匀加速直线运动穿出磁场;乙图为外力F随时间变化的图象.若线框的边长L、质量m、总电阻R及图象中的F0、t0均为已知量,则根据上述条件,请你求出匀强磁场的磁感应强度.
如图甲所示,一个正方形金属框位于有界匀强磁场区域内,线框的右边紧贴着边界,t=0时刻对线框施加一水平向右的外力F,让线框从静止开始做匀加速直线运动穿出磁场;乙图为外力F随时间变化的图象.若线框的边长L、质量m、总电阻R及图象中的F0、t0均为已知量,则根据上述条件,请你求出匀强磁场的磁感应强度.分析:根据牛顿第二定律与安培力大小公式,并结合运动学公式,即可求解.
解答:解:令线框做匀加速运动的加速度为a,t=t0时,对线框:由牛顿第二定律:
3F0-F安=ma …①
此时:F安 =BIL=
…②
0~t0时间内,由vt=at:所以v=at0 …③
t>t0后:由牛顿第二定律:F0=ma …④
联立方程组①~④,解出:B=
…⑤
另解:0~t0时间内,
由s=
at2;所以L=
a
=
…⑥
⑥代入⑤有B=
答:匀强磁场的磁感应强度B=
或B=
.
3F0-F安=ma …①
此时:F安 =BIL=
| B2L2v |
| R |
0~t0时间内,由vt=at:所以v=at0 …③
t>t0后:由牛顿第二定律:F0=ma …④
联立方程组①~④,解出:B=
|
另解:0~t0时间内,
由s=
| 1 |
| 2 |
| 1 |
| 2 |
| t | 2 0 |
| 1 |
| 2 |
| F0 |
| m |
| t | 2 0 |
⑥代入⑤有B=
| 2m | ||
F0
|
|
答:匀强磁场的磁感应强度B=
| 2m | ||
F0
|
|
|
点评:考查牛顿第二定律与运动学公式,掌握安培力的大小表达式,同时能理解另一种解法.

练习册系列答案
相关题目
 (2013?太原二模)如图甲所示,一个边长为L的正方形线框固定在匀强磁场(图中未画出)中,磁感应强度的方向垂直于导线框所在平面.规定向里为磁感应强度的正方向,向右为导线框ab边所受安培力的正方向.已知在0~4s时间内导线框ab边所受的安培力如图乙所示.则下列能正确表示磁感应强度B随时间变化的图象是( )
(2013?太原二模)如图甲所示,一个边长为L的正方形线框固定在匀强磁场(图中未画出)中,磁感应强度的方向垂直于导线框所在平面.规定向里为磁感应强度的正方向,向右为导线框ab边所受安培力的正方向.已知在0~4s时间内导线框ab边所受的安培力如图乙所示.则下列能正确表示磁感应强度B随时间变化的图象是( )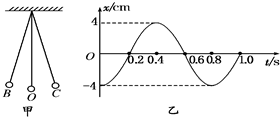 如图甲所示是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置.设摆球向右方向运动为正方向.图乙所示是这个单摆的振动图象.根据图象回答:(π2=10)
如图甲所示是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置.设摆球向右方向运动为正方向.图乙所示是这个单摆的振动图象.根据图象回答:(π2=10) )
)
 )
)
