题目内容
9．轻质细线吊着一质量为m=0.64kg、边长为L=0.8m的单匝正方形线圈abcd，线圈总电阻为R=1Ω．边长为d=0.4m的正方形磁场区域对称分布在线圈下边的两侧，如图（甲）所示．磁场方向垂直纸面向里，磁感应强度大小随时间变化如图（乙）所示，从t=0开始经t0时间细线开始松弛，取g=10m/s2．求：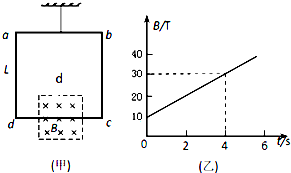
（1）线圈abcd中产生的感应电动势E和电功率P；
（2）求t0的值．
分析 （1）根据磁感应强度的变化，结合有效面积求出磁通量的变化量，根据法拉第电磁感应定律求出感应电动势的大小．根据P=I2R求出线圈abcd的电功率．
（2）当细线开始松弛，线框受重力和安培力平衡，根据平衡求出磁感应强度的大小，从而结合图线求出经历的时间．
解答 解：（1）由法拉第电磁感应定律E=$\frac{△∅}{△t}$
而△∅=$△B•\frac{{d}^{2}}{2}$
由乙图得
$\frac{△B}{△t}$=5T/s
解得：E=0.4V
而功率P=$\frac{{E}^{2}}{R}$
得P=0.16W
（2）在t0时刻mg=BId
再依据闭合电路欧姆定律，I=$\frac{E}{R}$
根据图象，B=10+5t0；
解得：t0=6s
答：（1）线圈abcd中产生的感应电动势0.4V和电功率0.16W；
（2）则t0的值6s．
点评 本题考查电磁感应与电路和基本力学的综合，难度不大，需加强训练．同时注意法拉第电磁感应定律与闭合电路欧姆定律的综合应用，掌握图象信息是解题的关键．
练习册系列答案
相关题目
9．如图所示，表示原子核的比结合能与质量数A的关系，据此下列说法中正确的是（ ）
| A． | 重的原子核，例如，铀核（${\;}_{92}^{235}$U），因为它的核子多，核力大，所以结合得坚固而稳定 | |
| B． | 锂核（${\;}_{3}^{6}$Li）的核子的比结合能比铀核的比结合能小，因而比铀核结合得更坚固更稳定 | |
| C． | 原子核结合的松紧程度可以用“比结合能”来表征，比结合能的定义是每个核子的平均结合能；比结合能越大的原子核越稳定 | |
| D． | 以上三个表述都错误 |
如图所示，粗细均匀的AB杆重100N，可绕A端转动，现将重量G1=200N的物体挂于杆的B端，并在中点C处用水平绳将杆拉住，已知AB杆与竖直方向夹角为60°，求水平绳的拉力F．
如图所示，在xOy平面内，以O1（0，R）为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1，x轴下方有一直线ab，ab与x轴相距为d，x轴与直线ab间区域有平行于y轴的匀强电场E，在ab的下方有一平行于x轴的感光板MN，ab与MN间区域有垂直于纸平面向外的匀强磁场B2．
4．
如图，两个初速度大小相同的不同粒子a和b，从O点沿垂直磁场方向进入匀强磁场，最后都打到屏上P点．不计重力．下列说法正确的有（ ）
如图，两个初速度大小相同的不同粒子a和b，从O点沿垂直磁场方向进入匀强磁场，最后都打到屏上P点．不计重力．下列说法正确的有（ ）| A． | a、b均带负电 | |
| B． | a在磁场中飞行的时间比b的短 | |
| C． | a在磁场做匀速圆周运支的角速度比b的大 | |
| D． | a的比荷（$\frac{q}{m}$）比b小 |
如图所示，两块水平放置的平行金属板M、N，相距为d，组成一个电容量为C的平行板电容器，现对电容器充电，使金属板M、N分别带上等量的负电和正电．M板正中央有一小孔B，从B孔正上方h处的A点，一质量为m、电量为+q的带电油滴自由下落后进入电容器内，不计空气阻力，重力加速度为g．问：
