题目内容
以v=20m/s的速度竖直上抛一小球，经2s以相同的初速度在同一点竖直上抛另一小球（g取10m/s2），则两球相碰处离出发点的高度是（ ）A．10m
B．15m
C．20m
D．不会相碰
【答案】分析：先判断先竖直上抛的小球到达最高点用的时间t=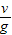
=2s，所以与另一小球相遇是在它的下落阶段，分别代入匀加速和竖直上抛运动规律即可．
解答：解：设第一个小球上升的最大高度为H，则由H=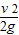
得：H=20m．
先判断先竖直上抛的小球到达最高点用的时间t=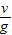
=2s，所以另一小球抛出时，它恰好在最高点将要做自由落体运动．
设：经过时间t相遇，则：
第一个小球下落的距离：h1=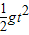
=5t2
第二个小球上升的高度：h2=vt-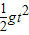
=20t-5t2
又因为：h1+h2=H代入数据得：
5t2+20t-5t2=20得：t=1s
所以：两球相碰处离出发点的高度h=vt-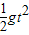
=20t-5t2=15m
故选：B
点评：竖直上抛运动是匀变速运动，特点是有一段往复，分析过程时可借助运动草图分析，找出需要的关系列式即可．
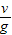=2s，所以与另一小球相遇是在它的下落阶段，分别代入匀加速和竖直上抛运动规律即可．解答：解：设第一个小球上升的最大高度为H，则由H=
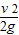得：H=20m．先判断先竖直上抛的小球到达最高点用的时间t=
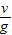=2s，所以另一小球抛出时，它恰好在最高点将要做自由落体运动．设：经过时间t相遇，则：
第一个小球下落的距离：h1=
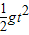=5t2第二个小球上升的高度：h2=vt-
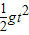=20t-5t2又因为：h1+h2=H代入数据得：
5t2+20t-5t2=20得：t=1s
所以：两球相碰处离出发点的高度h=vt-
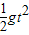=20t-5t2=15m故选：B
点评：竖直上抛运动是匀变速运动，特点是有一段往复，分析过程时可借助运动草图分析，找出需要的关系列式即可．
练习册系列答案
相关题目
的材料制成．一细束激光由其左端的中心点以α=45°的入射角射入光导纤维内，经过一系列全反射后从右端射出．求：
E．真空中的光速在不同的惯性参考系中都是相同的，与光源、观察者间的相对运动没有关系
(3)如图所示，一列简谐横波在t=0时刻的波的图象，A、B、C是介质中的三个质点。已知波是向x正方向传播的，波速为v=20m／s。请回答下列问题：