题目内容
3. 如图所示为一个盛有某种液体的槽,槽的中部扣着一个圆锥形薄壁透明罩,其侧视图为等边三角形ACB,罩内为空气,整个罩子恰好全部浸没在液体中,槽底AB的中点(即圆锥的底面圆心)处有一个点光源D,若槽内液体的折射率n=$\sqrt{\frac{7}{3}}$,等边三角形ACB的边长为a,要使点光源D发出的光不能射出液面,需要把圆锥形透明罩的上部从内部涂黑,试求:圆锥形透明罩上部涂黑的面积S.
如图所示为一个盛有某种液体的槽,槽的中部扣着一个圆锥形薄壁透明罩,其侧视图为等边三角形ACB,罩内为空气,整个罩子恰好全部浸没在液体中,槽底AB的中点(即圆锥的底面圆心)处有一个点光源D,若槽内液体的折射率n=$\sqrt{\frac{7}{3}}$,等边三角形ACB的边长为a,要使点光源D发出的光不能射出液面,需要把圆锥形透明罩的上部从内部涂黑,试求:圆锥形透明罩上部涂黑的面积S.
分析 根据题目已知条件作出光路图,通过折射率求出全反射的临界角,通过几何关系求出光发生全反射时在BC面上的入射角,通过数学几何知识求出圆锥形透明罩上部涂黑的面积S.
解答 解:光路图如图所示:
全反射临界角为C,$sinC=\frac{1}{n}$,
在P点,$n=\frac{sinα}{sinβ}$,C=60°-β,
联立解得$sinα=\frac{1}{2}$,则α=30°.
则P为BC边的中点,故涂黑部分的圆锥体的底面圆的半径$r=\frac{a}{4}$,母线$l=CP=\frac{a}{2}$,
则涂黑部分的面积为$S=πrl=\frac{π}{8}{a^2}$.
答:圆锥形透明罩上部涂黑的面积S为$\frac{π}{8}{a}^{2}$.
点评 解决本题的关键要掌握全反射的条件,要利用几何知识结合进行解答,正确作出光路图是基础,能熟练运用折射定律解答.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频交流电源两极相连,带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )


| A. | (t2-t1)=(t3-t2)=…=(tn-tn-1) | |
| B. | 高频交流电源的变化周期随粒子速度的增大而减小 | |
| C. | 要使粒子获得的最大动能增大,可以增大匀强磁场的磁感应强度 | |
| D. | 要使粒子获得的最大动能增大,可以减小粒子的比荷 |
11.质量为M的小车静止在水平地面上,当质量为m的人在小车上行走时,下列说法中正确的有( )
| A. | 若地面光滑,人和车组成的系统总动量方向与小车运动方向相同 | |
| B. | 若地面光滑,人和车组成的系统动量守恒 | |
| C. | 无论地面是否光滑,人和车组成的系统动量都一定守恒 | |
| D. | 只有当人的质量远远小于车的质量时,人和车组成的系统动量才守恒 |
8. 如图所示为地铁站用于安全检查的装置,主要由水平传送带和x光透视系统两部分组成,传送过程传送带速度不变.假设乘客把物品轻放在传送带上之后,物品总会先、后经历两个阶段的运动,用υ表示传送带速率,用μ表示物品与传送带间的动摩擦因数,则( )
如图所示为地铁站用于安全检查的装置,主要由水平传送带和x光透视系统两部分组成,传送过程传送带速度不变.假设乘客把物品轻放在传送带上之后,物品总会先、后经历两个阶段的运动,用υ表示传送带速率,用μ表示物品与传送带间的动摩擦因数,则( )
 如图所示为地铁站用于安全检查的装置,主要由水平传送带和x光透视系统两部分组成,传送过程传送带速度不变.假设乘客把物品轻放在传送带上之后,物品总会先、后经历两个阶段的运动,用υ表示传送带速率,用μ表示物品与传送带间的动摩擦因数,则( )
如图所示为地铁站用于安全检查的装置,主要由水平传送带和x光透视系统两部分组成,传送过程传送带速度不变.假设乘客把物品轻放在传送带上之后,物品总会先、后经历两个阶段的运动,用υ表示传送带速率,用μ表示物品与传送带间的动摩擦因数,则( )| A. | 前阶段,物品可能向传送方向的相反方向运动 | |
| B. | 后阶段,物品受到摩擦力的方向跟传送方向相同 | |
| C. | υ相同时,μ不同的等质量物品与传送带摩擦产生的热量相同 | |
| D. | μ相同时,υ增大为原来的2倍,前阶段物品的位移也增大为原来的2倍 |
20. 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形金属盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与金属盘接触良好的电刷A、B,当金属盘绕中心轴按图示方向转动时,则( )
法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形金属盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与金属盘接触良好的电刷A、B,当金属盘绕中心轴按图示方向转动时,则( )
 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形金属盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与金属盘接触良好的电刷A、B,当金属盘绕中心轴按图示方向转动时,则( )
法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形金属盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与金属盘接触良好的电刷A、B,当金属盘绕中心轴按图示方向转动时,则( )| A. | 若仅将滑动变阻器滑动头向左滑,灵敏电流计的示数将变大 | |
| B. | 电刷B的电势高于电刷A的电势 | |
| C. | 金属盘转动的转速越大,维持其做匀速转动所需外力做功的功率越小 | |
| D. | 若仅将电刷A向盘边缘移动,使电刷A、B之间距离增大,灵敏电流计的示数将变大 |
1.下列说法中正确的是( )
| A. | 爱因斯坦提出了光子说及光电效应方程,成功地解释了光电效应规律 | |
| B. | 汤姆逊通过阴极射线的研究发现了电子,并提了原子的核式结构模型 | |
| C. | 玻尔的原子理论成功地解释了氢原子光谱的实验规律 | |
| D. | 卢瑟福通过α粒子散射实验发现了质子 |
 如图所示,水平面上OM正中间有质量分别为2m、m的两物块B、C(中间粘有少量炸药),现引爆炸药,B、C被水平弹开,物块C运动到O点时,与刚好到达该点、质量为m、速度大小为v0的小物块A发生迎面正碰,碰后两者结合为一体向左滑动并刚好在M点与B相碰.不计一切摩擦,不计物体碰撞时间,三物块均可视为质点,重力加速度g=10m/s2.求:
如图所示,水平面上OM正中间有质量分别为2m、m的两物块B、C(中间粘有少量炸药),现引爆炸药,B、C被水平弹开,物块C运动到O点时,与刚好到达该点、质量为m、速度大小为v0的小物块A发生迎面正碰,碰后两者结合为一体向左滑动并刚好在M点与B相碰.不计一切摩擦,不计物体碰撞时间,三物块均可视为质点,重力加速度g=10m/s2.求: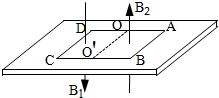 如图所示为磁悬浮列车模型,质量M=1.5kg的绝缘板底座与水平地面的动摩擦因数μ=0.1,正方形金属框ABCD固定在绝缘底座,其质量m=0.5kg,边长为1m,电阻为$\frac{1}{16}$Ω.OOˊ为AD、BC的中点.在金属框内有可随金属框同步移动的磁场,OOˊCD区域内磁场B1=kt,且k=0.5T/s,方向竖直向下;OOˊBA区域内磁场B2=2T,方向竖直向上.若AB恰在磁场边缘以内,CD边恰在磁场边缘以外,静止释放模型后,其加速度为3m/s2;若AB边和CD边恰都在磁场边缘以内,静止释放模型后,经过4s速度达到20m/s.(重力加速度g取10m/s2)
如图所示为磁悬浮列车模型,质量M=1.5kg的绝缘板底座与水平地面的动摩擦因数μ=0.1,正方形金属框ABCD固定在绝缘底座,其质量m=0.5kg,边长为1m,电阻为$\frac{1}{16}$Ω.OOˊ为AD、BC的中点.在金属框内有可随金属框同步移动的磁场,OOˊCD区域内磁场B1=kt,且k=0.5T/s,方向竖直向下;OOˊBA区域内磁场B2=2T,方向竖直向上.若AB恰在磁场边缘以内,CD边恰在磁场边缘以外,静止释放模型后,其加速度为3m/s2;若AB边和CD边恰都在磁场边缘以内,静止释放模型后,经过4s速度达到20m/s.(重力加速度g取10m/s2)