题目内容
13.如图所示,一根柔软的弹性绳子右端固定,左端自由,A、B、C、D…为绳上等间隔的点,相邻两点间间隔为50cm,现用手拉着绳子的端点A使其上下振动,若A点开始向上,经0.1s第一次达到最大位移,其数值为10cm,C点恰好开始振动,求:
(1)绳子形成的向右传播的横波速度为多大?
(2)从A开始振动,经多长时间K点第一次向上达到最大位移?
(3)在图示坐标系中画出当K点第一次向上达到最大位移时的波形图.
分析 (1)从A点开始振动到波传到C点所用时间为t=0.1s,传播的距离为x=2×50cm=1m,可由v=$\frac{x}{t}$求出波速.或求出周期,读出波长,再求波速.
(2)由波速和AK距离求出波从A点传到K点的时间,波刚传到K时,K也向上起振,再经过$\frac{1}{4}$T第一次到达波峰,两段时间之和即为所求.
(3)根据K质点的状态,画出波形.
解答 解:(1)由题意可得 $\frac{1}{4}$T=0.1s,故质点振动的周期T=0.4s; 由题意和图可得:$\frac{1}{4}$λ=1m,则波长λ=4m
故波速为:v=$\frac{λ}{T}$=10m/s.
(2)假设波由波源A传到K所用的时间为t1,则有:
t1=$\frac{{x}_{AK}}{v}$=$\frac{5}{10}$s=0.5s
假设波传到K到达正的最大位移需时间为t2,由于波源开始振动方向向上,故波传到K点时它先向上振动,则有:
t2=$\frac{1}{4}$T=$\frac{1}{4}$×0.4s=0.1s
所以对应总时间为:t=t1+t2=(0.5+0.1)s=0.6s.
(3)由(2)问可知:K第一次到达波峰的时间为0.6s,此时波前进的距离s=vt=10×0.6m=6m,即波此时到达M点,如图所示:
答:(1)绳子形成的向右传播的横波速度为10m/s.
(2)从A开始振动,经0.6s时间K点第一次向上达到最大位移.
(3)见解析图.
点评 本题关键利用波在同一介质中匀速传播和质点起振方向与波源起振方向相同的特点求出波速.分段求出波传到K点的时间.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
3.光电效应实验中,下列表述正确的是( )
| A. | 遏止电压与入射光的频率无关 | |
| B. | 入射光频率大于极限频率才能产生光电子 | |
| C. | 光照时间越长光电流越大 | |
| D. | 入射光足够强就可以有光电流 |
4.简单的、比较有效的电磁波的发射装置,至少应具备以下电路中的( )
①调谐电路;②调制电路;③高频振荡电路;④开放振荡电路.
①调谐电路;②调制电路;③高频振荡电路;④开放振荡电路.
| A. | ①②③ | B. | ②③④ | C. | ①④ | D. | ①②④ |
1.下面是某同学对电场中的一些概念及公式的理解,其中正确的是( )
| A. | 根据电场强度的定义式E=$\frac{F}{q}$可知,电场中某点的电场强度与试探电荷所带的电荷量成反比 | |
| B. | 根据电容的定义式C=$\frac{Q}{U}$ 可知,电容器的电容与其所带电荷量成正比,与两极板间的电压成反比 | |
| C. | 根据真空中点电荷的电场强度公式E=k$\frac{Q}{{r}^{2}}$可知,电场中某点的电场强度与场源电荷所带电荷量无关 | |
| D. | 根据电势差的定义式UAB=$\frac{{W}_{AB}}{q}$可知,带电荷量为1 C的正电荷,从A点移动到B点克服电场力做功为1 J,则A、B两点间的电势差为UAB=-1 V |
18. 在空间以水平面MN为界的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度恰好又水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可见( )
在空间以水平面MN为界的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度恰好又水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可见( )
 在空间以水平面MN为界的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度恰好又水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可见( )
在空间以水平面MN为界的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度恰好又水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可见( )| A. | 电场力为3mg | |
| B. | 小球带正电 | |
| C. | 小球从A到B与从B到C的时间相等 | |
| D. | 小球从A到B与从B到C的速度变化量相等 |
2.一定量的某种理想气体起始温度为T,体积为V,该气体在下面循环过程中经过三个平衡过程:(1)绝热膨胀到体积为2V;(2)等体变化使温度恢复为T.(3)等温压缩到原来体积V,则此整个循环过程中( )
| A. | 气体向外界放热 | B. | 气体对外界做正功 | ||
| C. | 气体内能增加 | D. | 气体内能减少 |
3.假设地球绕太阳运动时的轨道半径为r地,公转周期为T地,月球绕地球运动的轨道半径为r月,公转周期为T月,地球质量为M地,太阳质量为M阳,则关于轨道半径的三次方跟它的公转周期的二次方的比值k,下列说法不正确的是( )
| A. | 地球绕太阳运动的${k_地}=\frac{{G{M_阳}}}{{4{π^2}}}$ | B. | 月球绕地球运动的${k_月}=\frac{{G{M_月}}}{{4{π^2}}}$ | ||
| C. | $\frac{k_地}{k_月}=\frac{M_阳}{M_地}$ | D. | k只与中心天体的质量有关 |
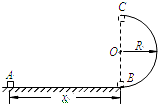 如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接,AB段长x=2.5m,半圆形轨道半径R=0.9m.质量m=0.10kg的小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,经B点时撤去力F,小滑块进入半圆形轨道,沿轨道恰好能运动到最高点C,然后从C点水平飞出.重力加速度g取10m/s2.求:
如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接,AB段长x=2.5m,半圆形轨道半径R=0.9m.质量m=0.10kg的小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,经B点时撤去力F,小滑块进入半圆形轨道,沿轨道恰好能运动到最高点C,然后从C点水平飞出.重力加速度g取10m/s2.求: