题目内容
7. 如图所示,倾角θ=30°的足够长平行导轨MN、M′N′与水平放置的平行导轨NP、N′P′平滑连接,导轨间距均为L,MM′间接有阻值为R的电阻,轨道光滑且电阻不计.倾斜导轨MN、M′N′之间(区域Ⅰ)有方向垂直导轨平面向上的匀强磁场,水平部分的ee′ff′之间(区域Ⅱ)有竖直向上的匀强磁场,磁场宽度为d.质量为m、电阻为r、长度略大于L的导体棒ab从靠近轨道上端的某位置由静止开始下滑,棒始终与导轨垂直并接触良好,经过ee′和ff′位置时的速率分别为v和$\frac{v}{4}$.已知导体棒ab进入区域Ⅱ运动时,其速度的减小量与它在磁场中通过的距离成正比,即△v∝△x.
如图所示,倾角θ=30°的足够长平行导轨MN、M′N′与水平放置的平行导轨NP、N′P′平滑连接,导轨间距均为L,MM′间接有阻值为R的电阻,轨道光滑且电阻不计.倾斜导轨MN、M′N′之间(区域Ⅰ)有方向垂直导轨平面向上的匀强磁场,水平部分的ee′ff′之间(区域Ⅱ)有竖直向上的匀强磁场,磁场宽度为d.质量为m、电阻为r、长度略大于L的导体棒ab从靠近轨道上端的某位置由静止开始下滑,棒始终与导轨垂直并接触良好,经过ee′和ff′位置时的速率分别为v和$\frac{v}{4}$.已知导体棒ab进入区域Ⅱ运动时,其速度的减小量与它在磁场中通过的距离成正比,即△v∝△x.(1)求区域Ⅰ匀强磁场的磁感应强度的大小.
(2)求导体棒ab通过区域Ⅱ过程中电阻R产生的焦耳热.
(3)改变区域Ⅰ的磁感应强度大小,使导体棒ab不能穿过区域Ⅱ,求区域Ⅰ的磁感应强度大小的取值范围.
分析 (1)由导体棒进入区域Ⅱ的速度得到在区域Ⅰ的最大速度,然后根据受力平衡列方程,求解方程即可;
(2)对导体棒进行受力分析,应用动能定理即可求解;
(3)由导体棒的速度变化量与位移的关系求得导体棒不能通过区域Ⅱ的初速度范围,然后根据受力平衡求得区域Ⅰ的磁感应强度范围.
解答 解:(1)导体棒在磁场区域Ⅰ和磁场区域Ⅱ之间运动时,在水平方向上没有外力,故导体棒做匀速直线运动;
导体棒在斜面上下滑时,受重力、支持力、安培力作用,导轨足够长,则导体棒到达NN′前已达到最大速度,即导体棒在斜面上达到最大速度v时,导体棒受力平衡,则有:
$mgsinθ={B}_{1}IL=\frac{{{B}_{1}}^{2}{L}^{2}v}{R+r}$
解得:${B}_{1}=\sqrt{\frac{mg(R+r)sinθ}{{L}^{2}v}}$=$\frac{1}{L}\sqrt{\frac{mg(R+r)}{2v}}$;
(2)导体棒在区域Ⅱ中运动,只有安培力做功,所以,克服安培力做功为:
$W=\frac{1}{2}m{v}^{2}-\frac{1}{2}m(\frac{1}{4}v)^{2}=\frac{15}{32}m{v}^{2}$;
所以,整个闭合电路产生的焦耳热为W,那么由串联电路的焦耳定律可知:电阻R产生的焦耳热为:
$Q=\frac{R}{R+r}W=\frac{15m{v}^{2}R}{32(R+r)}$;
(3)已知导体棒ab进入区域Ⅱ运动时,其速度的减小量与它在磁场中通过的距离成正比,即△v∝△x,
则有:$v-\frac{1}{4}v=kd$;
若导体棒以速度v′进入磁场区域Ⅱ,导体棒不能穿过区域Ⅱ,则:
有$v′-0<kd=v-\frac{1}{4}v=\frac{3}{4}v$;
由(1)可知:${B}_{1}′=\frac{1}{L}\sqrt{\frac{mg(R+r)}{2v′}}>\frac{1}{L}\sqrt{\frac{2mg(R+r)}{3v}}$;
答:(1)区域Ⅰ匀强磁场的磁感应强度的大小为$\frac{1}{L}\sqrt{\frac{mg(R+r)}{2v}}$;
(2)导体棒ab通过区域Ⅱ过程中电阻R产生的焦耳热为$\frac{15m{v}^{2}R}{32(R+r)}$;
(3)改变区域Ⅰ的磁感应强度大小,使导体棒ab不能穿过区域Ⅱ,则区域Ⅰ的磁感应强度大小大于$\frac{1}{L}\sqrt{\frac{2mg(R+r)}{3v}}$.
点评 闭合电路切割磁感线的问题中,一般由速度求得电动势,再根据电路求得电流,进而得到安培力;然后对导体棒进行受力分析,即可应用牛顿第二定律联系导体棒的运动状态,或应用动能定理求取安培力做功.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 小物块释放的高度为$\frac{5}{2}$R | B. | DE间的距离为$\frac{3R}{2μ}$ | ||
| C. | 小物块在DE间运动的路程为$\frac{5R}{μ}$ | D. | 小物块与小球共发生4次碰撞 |
 如图所示,一个由导体做成的矩形线圈,以恒定速率v运动,从无场区进入匀强磁场区,然后出来,若取逆时针方向为电流的正方向,那么图中所示的哪一个图象正确地表示回路中电流对时间的函数关系( )
如图所示,一个由导体做成的矩形线圈,以恒定速率v运动,从无场区进入匀强磁场区,然后出来,若取逆时针方向为电流的正方向,那么图中所示的哪一个图象正确地表示回路中电流对时间的函数关系( )| A. |  | B. |  | C. |  | D. |  |
| A. | “天宫一号”内的仪器由于完全失重惯性消失了 | |
| B. | 同一物体在月球表面上的重力只有地面上的$\frac{1}{6}$,但是惯性没有变化 | |
| C. | 运动员掷铁饼时带动铁饼快速旋转可增大铁饼的惯性 | |
| D. | 磁悬浮列车能高速行驶是因为列车浮起后惯性减小了 |
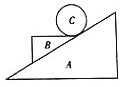 如图所示,光滑水平地面上有一倾斜角为30°的斜面体A,三角形木块B静止在A上,木块B上表面水平,将光滑小球C放置于木块B上,A、B、C的质量均为1kg,斜面体A在水平外力F作用下以3m/s2的加速度向左加速运动,运动过程中A、B、C始终相对静止,g取10m/s2.则( )
如图所示,光滑水平地面上有一倾斜角为30°的斜面体A,三角形木块B静止在A上,木块B上表面水平,将光滑小球C放置于木块B上,A、B、C的质量均为1kg,斜面体A在水平外力F作用下以3m/s2的加速度向左加速运动,运动过程中A、B、C始终相对静止,g取10m/s2.则( )| A. | 小球C受到两个作用力 | B. | 小球C受到三个作用力 | ||
| C. | 小球B受到三个作用力 | D. | 力F大小为9N |
 如图所示,有一底面直径和高都是d的空圆筒.当眼放在A点时恰能看到筒底B点,若在圆筒内倒满某种液体,在A点沿原方向看去,恰能看到圆心C,则液体的折射率是1.58.
如图所示,有一底面直径和高都是d的空圆筒.当眼放在A点时恰能看到筒底B点,若在圆筒内倒满某种液体,在A点沿原方向看去,恰能看到圆心C,则液体的折射率是1.58. 如图所示,导体棒ef置于固定在水平面上的U形金属框架abcd上,并良好接触,整个装置处在竖直向下的匀强磁场中.t=0时,磁感应强度为B0,aefc恰构成一个正方形回路,导体棒在水平拉力作用下由静止开始向右做匀加速直线运动,为使回路中不产生感应电流,磁感应强度B随时间t变化的规律应为图中的哪一个( )
如图所示,导体棒ef置于固定在水平面上的U形金属框架abcd上,并良好接触,整个装置处在竖直向下的匀强磁场中.t=0时,磁感应强度为B0,aefc恰构成一个正方形回路,导体棒在水平拉力作用下由静止开始向右做匀加速直线运动,为使回路中不产生感应电流,磁感应强度B随时间t变化的规律应为图中的哪一个( )



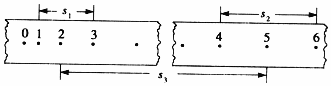 在“利用电火花打点计时器测定小车做匀变速运动的加速度”的实验中,下述器材中不需要的是①④⑧(用代号表示).
在“利用电火花打点计时器测定小车做匀变速运动的加速度”的实验中,下述器材中不需要的是①④⑧(用代号表示).