题目内容
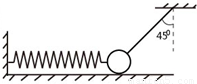
在动摩擦因数μ=0.2的水平面上有一个质量为m=1kg的小球，小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连，如图所示，此时小球处于静止平衡状态，且水平面对小球的弹力恰好为零，当剪断轻绳的瞬间，取g=10m/s2，求：（1）此时轻弹簧的弹力大小
（2）小球的加速度大小和方向．
【答案】分析：先分析剪断轻绳前弹簧的弹力和轻绳的拉力大小，再研究剪断轻绳瞬间，抓住弹簧的弹力没有变化，求解小球的合力，由牛顿第二定律求出小球的加速度的大小和方向．
解答：解：（1）水平面对小球的弹力为零，小球在绳没有断时受到绳的拉力F、重力mg和弹簧的弹力T作用而处于平衡状态，如图所示：
由平衡条件得：
竖直方向：Fcosθ=mg
水平方向：Fsinθ=T
解得：T=mgtanθ=10N
当剪断轻绳瞬间弹簧的弹力大小不变，仍为10N；
（2）剪断轻绳后小球在竖直方向仍平衡，
水平面支持力与重力平衡：N=mg
由牛顿第二定律得：T-μN=ma
解得：a=8m/s2 方向向左．
答：（1）此时轻弹簧的弹力大小为10N；
（2）小球的加速度大小为8m/s2，方向向左．
点评：本题是瞬时问题，先分析剪断轻绳前小球的受力情况，再分析剪断轻绳瞬间的受力情况，再根据牛顿第二定律求解瞬间的加速度．
解答：解：（1）水平面对小球的弹力为零，小球在绳没有断时受到绳的拉力F、重力mg和弹簧的弹力T作用而处于平衡状态，如图所示：
由平衡条件得：
竖直方向：Fcosθ=mg
水平方向：Fsinθ=T
解得：T=mgtanθ=10N
当剪断轻绳瞬间弹簧的弹力大小不变，仍为10N；
（2）剪断轻绳后小球在竖直方向仍平衡，
水平面支持力与重力平衡：N=mg
由牛顿第二定律得：T-μN=ma
解得：a=8m/s2 方向向左．
答：（1）此时轻弹簧的弹力大小为10N；
（2）小球的加速度大小为8m/s2，方向向左．
点评：本题是瞬时问题，先分析剪断轻绳前小球的受力情况，再分析剪断轻绳瞬间的受力情况，再根据牛顿第二定律求解瞬间的加速度．
练习册系列答案
相关题目
（2012?上海模拟）在动摩擦因数μ=0.2的粗糙绝缘足够长的水平滑漕中，长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B，如图为俯视图（槽两侧光滑）．A球的电荷量为+2q，B球的电荷量为-3q（均可视为质点，也不考虑两者间相互作用的库仑力）．现让A处于如图所示的有界匀强电场区域MPQN内，已知虚线MP恰位于细杆的中垂线，MP和NQ的距离为3L，匀强电场的场强大小为E=1.2mg/q，方向水平向右．释放带电系统，让A、B从静止开始运动（忽略小球运动中所产生的磁场造成的影响）．求：
如图所示，在动摩擦因数μ=0.2的水平面AB上，水平恒力F （F大小未知）推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动，物体到达B点时撤去F，接着又冲上光滑斜面（设经过B点前后速度大小不变），最高能到达C点．用速度传感器测量物体的瞬时速度，并在表格中记录了部分测量数据（g取10m/s2）．
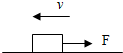一物体在动摩擦因数μ=0.2的水平面上向左运动，物体的质量为10kg，它在运动过程当中还受到一个水平向右的大小为20N的拉力作用，则物体受到的摩擦力为（ ）| A、0N | B、20N，水平向右 | C、40N，水平向右 | D、20N，水平向左 |
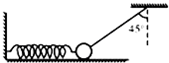如图所示，在动摩擦因数μ=0.2的水平面上有一个质量m=1kg的小球，小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连，此时小球处于静止状态，且水平面对小球的弹力恰好为零．在剪断轻绳的瞬间（g取10m/s2），下列说法中正确的是（ ）| A、小球受力个数不变 | ||
| B、小球立即向左运动，且a=8m/s2 | ||
| C、小球立即向左运动，且a=10m/s2 | ||
D、若剪断的是弹簧，则剪断瞬间时小球加速度的大小a=10
|
（2010?黑龙江模拟）（按题目要求作答，写出必要的文字说明、方程式和重要演算步骤，只写出最后答案不得分）