题目内容
如图所示,质量均为m的A、B两个弹性小球,用长为2l不可伸长的轻绳连接,现把AB两球置于距地面高H处(H足够大)间距为l,当A球自由下落的同时,B球以速度v0指向A球水平抛出,求:

(1)两球从开始运动到相碰,A球下落的高度;
(2)A、B两球碰撞(碰撞时无机械能损失)后,各自速度的水平分量;
(3)轻绳拉直过程中,B球受到绳子拉力冲量的大小.
【答案】
(1) (2)vAx′=v0 vBx′=0 (3)
(2)vAx′=v0 vBx′=0 (3)
【解析】
试题分析:(1)设A球下落的高度为h
l=v0t ①
h= ②
②
联立①②两式得 h= ③
③
(2)由水平方向动量守恒知mv0=mvAx′+mvBx ′④
由机械能守恒知
 )+
)+ =
= m(
m( )+
)+ ⑤
⑤
式中
联立④⑤得 
(3)由水平方向动量守恒得
故 =
=
考点:平抛运动规律 动量守恒定律 机械能守恒
点评:本题属于综合型题目,既考到曲线运动又包括水平方向动量守恒问题,学生们要注意当碰撞的系统所受合外力不为零时,可能某一方向合力为零,这个时侯该方向动量守恒。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 (2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( )
(2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( ) 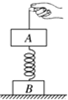 如图所示,质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A缓慢地向上拉起,当B刚要离开地面时,求A上升距离(假设弹簧一直在弹性限度内,重力加速度g已知)
如图所示,质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A缓慢地向上拉起,当B刚要离开地面时,求A上升距离(假设弹簧一直在弹性限度内,重力加速度g已知)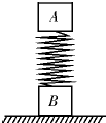 (2013?湖南模拟)如图所示,质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端,当A静止时弹簧的压缩量为l.现用一竖直向下的恒力F=3mg作用于A上,当A运动一段距离x,后撤去F,结果B刚好不离开水平面,则l:x的值为( )
(2013?湖南模拟)如图所示,质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端,当A静止时弹簧的压缩量为l.现用一竖直向下的恒力F=3mg作用于A上,当A运动一段距离x,后撤去F,结果B刚好不离开水平面,则l:x的值为( )