Question

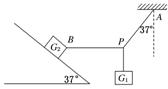
所受重力G₁＝8 N的砝码悬挂在绳PA和PB的结点上,PA偏离竖直方向37°角，PB在水平方向，且连在所受重力为G₂＝100 N的木块上，木块静止于倾角为37°的斜面上，如图所示，试求：

(1) PA、PB绳上的拉力分别为多大？

(2)木块与斜面间的摩擦力？(3)木块所受斜面的弹力？

Answer 1

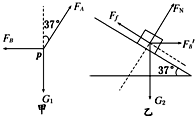
解：（1）如图甲所示分析P点受力，由平衡条件可得：
F_A cos37°=G₁    F_A sin37°=F_B
可解得：F_B=6 N   
(2)再分析G₂的受力情况，如图乙所示
由物体的平衡条件可得：
F_f=G₂ sin37°+F_B′cos37°
F_N+F_B′sin37°=G₂ cos37°
F_B′=F_B     可求得：F_f=64.8 N    F_N=76.4 N
即木块与斜面间的摩擦力大小为64.8N； F_N=76.4 N
即木块所受斜面的弹力大小为76.4 N．