题目内容
（2010?天津）探测器绕月球做匀速圆周运动，变轨后在周期较小的轨道上仍做匀速圆周运动，则变轨后与变轨前相比（ ）
分析：根据万有引力提供向心力列式求解即可得到线速度、角速度、周期、向心加速度与轨道半径的关系；根据周期变小，先得到轨道半径的变化，再得出其它量的变化．
解答：解：由于G
=m(
)2r，所以r=
，T变小，r变小，A正确．
又G
=man，an=
，r变小，an增大，B错误．
由G
=m
，v=
，r变小，v增大，C错误．
由G
=mω2r，ω=
，r变小，ω增大，D错误
故选A．
| Mm |
| r2 |
| 2π |
| T |
| 3 |
| ||
又G
| Mm |
| r2 |
| GM |
| r2 |
由G
| Mm |
| r2 |
| v2 |
| r |
|
由G
| Mm |
| r2 |
|
故选A．
点评：人造卫星的线速度、角速度、周期、向心加速度只与轨道半径有关，与卫星的质量无关！
练习册系列答案
相关题目
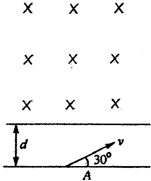（2010?天津模拟）如图所示宽度为d的区域上方存在垂直纸面、方向向内、磁感应强度大小为B的无限大匀强磁场，现有一质量为m，带电量为+q的粒子在纸面内以某一速度从此区域下边缘上的A点射入，其方向与下边缘线成30°角，粒子能回到A点，（不计重力）试求：（2010·天津卷）6.探测器绕月球做匀速圆周运动，变轨后在周期较小的轨道上仍做匀速圆周运动，则变轨后与变轨前相比（ ）
| A．轨道半径变小 | B．向心加速度变小 |
| C．线速度变小 | D．角速度变小 |