题目内容
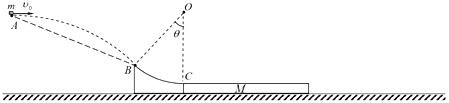
【题目】如图，光滑半圆形轨道处于竖直平面内，半圆形轨道与光滑的水平地面相切于半圆的端点A．一质量为m的小球在水平地面上C点受水平向左的恒力F由静止开始运动，当运动到A点时撤去恒力F，小球沿竖直半圆形轨道运动到轨道最高点B点，最后又落在水平地面上的D点（图中未画出）．已知A、C间的距离为L，重力加速度为g．
（1）若轨道半径为R，求小球到达半圆形轨道B点时对轨道的压力FN；
（2）为使小球能运动到轨道最高点B，求轨道半径的最大值Rm；
（3）当轨道半径
时，小球在水平地面上的落点D到A点距离是多少？
【答案】(1)
(2)
(3)
【解析】
(1)设小球到B点速度为v，从C到B根据动能定理有
解得
在B点，由牛顿第二定律有
解得
根据牛顿第三定律可知
(2)小球恰能运动到轨道最高点时，轨道半径有最大值，则有
解得
(3) 设小球平抛运动的时间为t，有
解得
水平位移
将轨道半径
代入得
练习册系列答案
阅读快车系列答案
相关题目
