题目内容
如图所示,将悬线拉至水平位置无初速度释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,则在悬线被钉子挡住的前后瞬间相比较,不计空气阻力.则( )
A.小球的角速度变大
B.小球的动能减小
C.悬线的张力不变
D.小球的向心加速度变小
【答案】分析:当小球达到最低时,细线被钉子拦住的瞬间,小球的线速度是不变的.由于细线被挡住导致半径变小,由线速度、角速度与半径的关系可得出小球的角速度、向心加速度及动能的变化情况,同时在最低点由向心力公式结合牛顿第二定律可知悬线的拉力如何变化.
解答:解:当悬线碰到钉子瞬间时,小球的线速度是不变的.由于悬线被挡时导致半径减小,则:
A、因为r减小,则由v=ωr得,角速度ω变大.故A正确;
B、因为线速度v不变,所以小球的动能也不变.故B不正确;
C、小球在最低点受重力与拉力,因为m、v、g是不变的,而r减小,由T-mg=m 得:T变大.故C不正确;
得:T变大.故C不正确;
D、因为线速度 v不变,半径r变小,由an=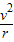 得:an变大,故不正确;
得:an变大,故不正确;
故选A.
点评:考查线速度、角速度与半径的关系及向心力的公式,同时体现了牛顿第二定律.本题突破口是当悬线碰到钉子时,线速度是不变的.
解答:解:当悬线碰到钉子瞬间时,小球的线速度是不变的.由于悬线被挡时导致半径减小,则:
A、因为r减小,则由v=ωr得,角速度ω变大.故A正确;
B、因为线速度v不变,所以小球的动能也不变.故B不正确;
C、小球在最低点受重力与拉力,因为m、v、g是不变的,而r减小,由T-mg=m
 得:T变大.故C不正确;
得:T变大.故C不正确;D、因为线速度 v不变,半径r变小,由an=
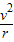 得:an变大,故不正确;
得:an变大,故不正确;故选A.
点评:考查线速度、角速度与半径的关系及向心力的公式,同时体现了牛顿第二定律.本题突破口是当悬线碰到钉子时,线速度是不变的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,比较悬线被小钉子挡住的前后瞬间( )
如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,比较悬线被小钉子挡住的前后瞬间( ) (2013?高淳县模拟)如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住的瞬间速度的大小不变,比较悬线被小钉子挡住的前后瞬间,
(2013?高淳县模拟)如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住的瞬间速度的大小不变,比较悬线被小钉子挡住的前后瞬间, 如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线突然断裂,则( )
如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线突然断裂,则( ) 如图所示,将悬线拉至水平位置无初速度释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,则在悬线被钉子挡住的前后瞬间相比较,不计空气阻力.则( )
如图所示,将悬线拉至水平位置无初速度释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,则在悬线被钉子挡住的前后瞬间相比较,不计空气阻力.则( )