题目内容
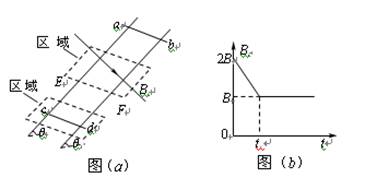
如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面向上的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如下图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知cd棒的质量为m、电阻为R,ab棒的质量未知、阻值为r,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求:
(1)ab棒进入区域Ⅱ之前cd棒上的感应电流的方向及大小
(2)ab棒进入区域Ⅱ时的速度大小及进入时刻tx
(3)ab棒从开始下滑至EF的过程中回路中产生的热量.
(1)ab棒进入区域Ⅱ之前cd棒上的感应电流的方向及大小
(2)ab棒进入区域Ⅱ时的速度大小及进入时刻tx
(3)ab棒从开始下滑至EF的过程中回路中产生的热量.

(1)cd棒处于静止状态,其受力如图,由左手定则判断知cd棒上的感应电流方向为:d到c.

对cd棒,由平衡条件,得mgsinθ=BIL ①
解得 I=
(2)设ab棒以速度v进入区域Ⅱ将做匀速直线运动,由闭合回路的欧姆定律得:
=I ②
解得 v=
ab棒未进入区域Ⅱ时做匀加速直线运动,得 mgsinθ=ma ③
v=atx ④
解得 tx=
(3)因回路中电流是恒定电流,则 Q=I2(R+r)(tx+
) ⑤
解得Q=
+2mgLsinθ
答:
(1)ab棒进入区域Ⅱ之前cd棒上的感应电流的方向d到c,大小为
.
(2)ab棒进入区域Ⅱ时的速度大小及进入时刻tx
.
(3)ab棒从开始下滑至EF的过程中回路中产生的热量为
+2mgLsinθ.

对cd棒,由平衡条件,得mgsinθ=BIL ①
解得 I=
| mgsinθ |
| BL |
(2)设ab棒以速度v进入区域Ⅱ将做匀速直线运动,由闭合回路的欧姆定律得:
| BLv |
| R+r |
解得 v=
| mg(R+r)sinθ |
| B2L2 |
ab棒未进入区域Ⅱ时做匀加速直线运动,得 mgsinθ=ma ③
v=atx ④
解得 tx=
| m(R+r) |
| B2L2 |
(3)因回路中电流是恒定电流,则 Q=I2(R+r)(tx+
| 2L |
| v |
解得Q=
| m3g2(R+r)2sin2θ |
| B4L4 |
答:
(1)ab棒进入区域Ⅱ之前cd棒上的感应电流的方向d到c,大小为
| mgsinθ |
| BL |
(2)ab棒进入区域Ⅱ时的速度大小及进入时刻tx
| m(R+r) |
| B2L2 |
(3)ab棒从开始下滑至EF的过程中回路中产生的热量为
| m3g2(R+r)2sin2θ |
| B4L4 |

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
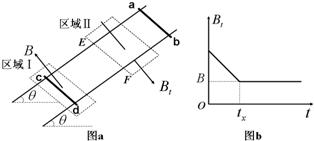 如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面向上的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如下图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知cd棒的质量为m、电阻为R,ab棒的质量未知、阻值为r,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求:
如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面向上的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如下图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知cd棒的质量为m、电阻为R,ab棒的质量未知、阻值为r,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求: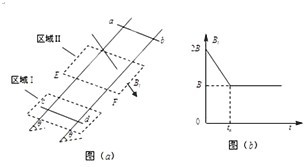 如图(a)所示,间距为L电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.又已知cd棒的质量为m,区域Ⅱ沿斜面的长度也是L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求:
如图(a)所示,间距为L电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.又已知cd棒的质量为m,区域Ⅱ沿斜面的长度也是L,在t=tx时刻(tx未知)ab棒恰好进入区域Ⅱ,重力加速度为g.求: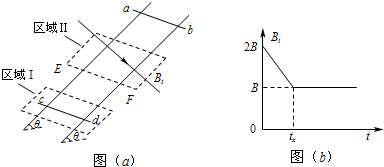 (2011?虹口区二模)如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.
(2011?虹口区二模)如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度恒为B不变;在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放.在ab棒运动到区域Ⅱ的下边界EF之前,cd棒始终静止不动,两棒均与导轨接触良好.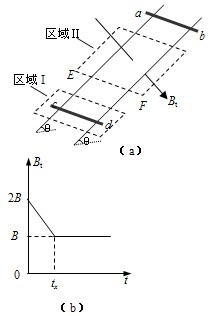 如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下区域I区域Ⅱ有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.
如图(a)所示,间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上.在区域I内有方向垂直于斜面的匀强磁场,磁感应强度为B;在区域Ⅱ内有垂直于斜面向下区域I区域Ⅱ有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.