题目内容
如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期都相同,则( )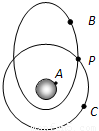
A.相对于地心,卫星C的运行速度大于物体A的速度
B.相对于地心,卫星C的运行速度等于物体A的速度
C.卫星B在P点的加速度大小大于卫星C在该点加速度
D.卫星B在P点的加速度大小等于卫星C在该点加速度大小
【答案】分析:根据A、C的周期相等,知角速度相等,通过v=rω比较A、C速度的大小.因为卫星的周期一定,根据万有引力提供向心力确定其轨道半径一定.根据卫星所受的万有引力,通过牛顿第二定律比较加速度的大小.
解答:解:A、物体A和卫星C的周期相等,则角速度相等,根据v=rω知,半径越大,线速度越大.所以卫星C的运行速度大于物体A的速度.故A正确,B错误
C、根据a=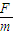 =
=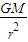 知,两卫星距离地心的距离相等,则加速度相等.故C错误,D正确.
知,两卫星距离地心的距离相等,则加速度相等.故C错误,D正确.
故选AD.
点评:解决本题的关键知道A和C的角速度相等,通过v=rω 比较线速度大小,注意物体A随地球做圆周运动不是靠万有引力提供向心力.
解答:解:A、物体A和卫星C的周期相等,则角速度相等,根据v=rω知,半径越大,线速度越大.所以卫星C的运行速度大于物体A的速度.故A正确,B错误
C、根据a=
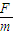 =
=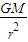 知,两卫星距离地心的距离相等,则加速度相等.故C错误,D正确.
知,两卫星距离地心的距离相等,则加速度相等.故C错误,D正确.故选AD.
点评:解决本题的关键知道A和C的角速度相等,通过v=rω 比较线速度大小,注意物体A随地球做圆周运动不是靠万有引力提供向心力.

练习册系列答案
相关题目
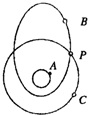 如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道 的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道 的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )| A、卫星C的运行速度大于物体A的速度 | B、物体A和卫星C具有相同大小的加速度 | C、卫星B在近地点的速度大于卫星C的速度 | D、卫星B在P点的加速度与卫星C在该点加速度不相等 |
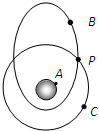 如图所示,A为静止于地球赤道上未发射的卫星,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.下列说法中正确的是( )
如图所示,A为静止于地球赤道上未发射的卫星,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.下列说法中正确的是( ) 如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C运动的周期相同,则( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C运动的周期相同,则( ) 如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )