题目内容
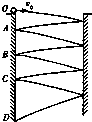如图所示，一可视为质点的小球以初速度v0从O点水平抛出，经与两墙壁七次碰撞后刚好落在竖直墙壁的最低点D，此时速度与水平方向的夹角为θ，其中A、C两点为小球与另一墙壁碰撞的等高点，已知两墙壁间的距离为d，与墙壁碰撞无能量损失，且速度满足光的反射规律，则下列说法不正确的是（ ）分析：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据两墙壁间的距离求出在两墙壁间水平方向上的运动时间，从而得出运动的总时间，结合平抛运动的规律求出速度与水平方向的夹角的正切值．
解答：解：A、小球在水平方向上速度的大小相等，根据等时性知，OA、AB、BC、CD时间相等，在竖直方向上做自由落体运动，根据初速度为零的匀变速直线运动的推论，知xOA：xAB：xBC：xCD=1：3：5：7．故A正确．
B、因为在相邻两点间所需的时间相等，水平方向上的速度大小不变，竖直方向上做自由落体运动，则相邻两点间的速度变化量相等．故B正确．
C、小球从O点运动到D点的时间t=
，则tanθ=
=
=
．故C、D错误．
本题选错误的，故选CD．
B、因为在相邻两点间所需的时间相等，水平方向上的速度大小不变，竖直方向上做自由落体运动，则相邻两点间的速度变化量相等．故B正确．
C、小球从O点运动到D点的时间t=
| 8d |
| v0 |
| gt |
| v0 |
| ||
| v0 |
| 8gd |
| v02 |
本题选错误的，故选CD．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，抓住等时性，结合运动学公式进行求解．
练习册系列答案
相关题目
如图所示，一根轻质弹簧上端固定，不挂重物时下端位置为C点；在下端挂一个质量为m的物体（可视为质点）后再次保持静止，此时物体位于A点；将物体向下拉至B点后释放，关于物体的运动情况，下面说法中不正确的是（ ）
