题目内容
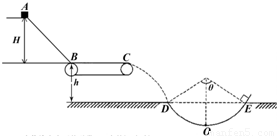
如图所示，设AB段是距水平传送带装置高为H＝1.25 m的光滑斜面，水平段BC使用水平传送带装置，BC长L＝5 m，与货物包的摩擦系数为μ＝0.4，顺时针转动的速度为V＝3 m/s．设质量为m＝1 kg的小物块由静止开始从A点下滑，经过B点的拐角处无机械能损失．小物块随传送带运动到C点后水平抛出，恰好无碰撞的沿圆弧切线从D点进入竖直光滑圆孤轨道下滑．D、E为圆弧的两端点，其连线水平．已知圆弧半径R2＝1.0 m圆弧对应圆心角＝106°，O为轨道的最低点．(g＝10 m/s2，sin37°＝0.6，cos37°＝0.8)试求：
(1)小物块在B点的速度．
(2)小物块在水平传送带BC上的运动时间．
(3)水平传送带上表面距地面的高度．
(4)小物块经过O点时对轨道的压力．
答案：
解析：
解析：
|
(1) (2)1.5 s (3)0.8 m (4)43 N (1)小物块由A运动B，由动能定理， 解得： (2)由牛顿第二定律，得 水平传送带的速度为 由 (2)小物块从C到D做平抛运动，在D点有有： 由 (3)小物块在D点的速度大小为： 对小物块从D点到O由动能定理，得： 在O点由牛顿第二定律，得： 联立以上两式解得： 由牛顿第三定律知对轨道的压力为： |
，解得：
(1分)
，得：
，则
(1分)，
，
(2分)
(1分)
(1分)，得
(2分)
(1分)
(1分)
＝43 N(1分)
(1分)
练习册系列答案
阅读快车系列答案
相关题目
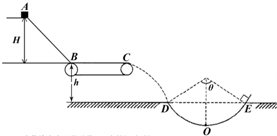（学有余力同学做，不计入总分）如图所示，设AB段是距水平传送带装置高为H=1.25m的光滑斜面，水平段BC使用水平传送带装置，BC长L=5m，与货物包的摩擦系数为μ=0.4，顺时针转动的速度为V=3m/s．设质量为m=1kg的小物块由静止开始从A点下滑，经过B点的拐角处无机械能损失．小物块随传送带运动到C点后水平抛出，恰好无碰撞的沿圆弧切线从D点进入竖直光滑圆孤轨道下滑．D、E为圆弧的两端点，其连线水平．已知圆弧半径R2=1.0m圆弧对应圆心角θ=106°，O为轨道的最低点．（g=10m/s2，sin37°=0.6，cos37°=0.8）试求：
，O为轨道的最低点。（g=10m/s2，sin37°=0.6，cos37°=0.8）试求：
