题目内容
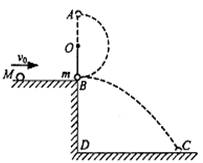
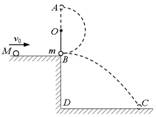
 如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为l=0.60m.平台高BD=0.80m.一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m.求:质量为M的小球与摆球碰撞前的速度大小.
如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为l=0.60m.平台高BD=0.80m.一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m.求:质量为M的小球与摆球碰撞前的速度大小.
【答案】分析:以摆球为研究对象,当它经最高点A时,绳上的拉力T恰好等于摆球的重力,由重力与拉力的合力提供小球的向心力,根据牛顿第二定律求出摆球经过最高点的速度大小,由机械能守恒定律求出摆球在最低点的速度.以小球研究对象,由平抛运动知识求出入碰撞后小球做平抛运动的初速度,再根据动量守恒定律求解小球与摆球碰撞前的速度大小.
解答:解:以摆球m为研究对象,在最高点时,对球受力分析,受重力mg和拉力T,由牛顿第二定律得:
mg+T=m
因T=mg
则:2mg=m
得:
在摆球由最低点到最高点的过程中,根据机械能守恒定律得:
mg?2l+ =
=
解得:vB= =
= =6m/s.
=6m/s.
对于小球M:碰撞后M做平抛运动,则有:
竖直方向:h=
水平方向:
代入解得,碰撞后M的速度大小为:v=3m/s
两球碰撞过程中,合外力为零,根据动量守恒定律得:
Mv=Mv+mvB
代入解得,v=6m/s
答:质量为M的小球与摆球碰撞前的速度大小为6m/s.
点评:本题是碰撞、平抛运动与圆周运动和综合,采用程序法思维,把握各个运动过程的物理规律是关键.
解答:解:以摆球m为研究对象,在最高点时,对球受力分析,受重力mg和拉力T,由牛顿第二定律得:
mg+T=m

因T=mg
则:2mg=m

得:

在摆球由最低点到最高点的过程中,根据机械能守恒定律得:
mg?2l+
 =
=
解得:vB=
 =
= =6m/s.
=6m/s.对于小球M:碰撞后M做平抛运动,则有:
竖直方向:h=

水平方向:

代入解得,碰撞后M的速度大小为:v=3m/s
两球碰撞过程中,合外力为零,根据动量守恒定律得:
Mv=Mv+mvB
代入解得,v=6m/s
答:质量为M的小球与摆球碰撞前的速度大小为6m/s.
点评:本题是碰撞、平抛运动与圆周运动和综合,采用程序法思维,把握各个运动过程的物理规律是关键.

练习册系列答案
相关题目
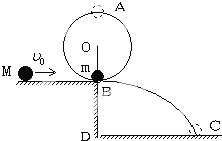 如图所示,O为一水平轴.细绳的一端固定于O点,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为L=0.6米.平台高BD=0.8米.一个质量为M=3.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳子的约束下做圆周运动,经最高点A时,绳子的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2米.求:
如图所示,O为一水平轴.细绳的一端固定于O点,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为L=0.6米.平台高BD=0.8米.一个质量为M=3.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳子的约束下做圆周运动,经最高点A时,绳子的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2米.求: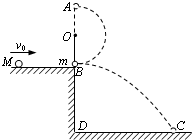 如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为l=0.60m.平台高BD=0.80m.一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m.求:质量为M的小球与摆球碰撞前的速度大小.
如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为l=0.60m.平台高BD=0.80m.一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m.求:质量为M的小球与摆球碰撞前的速度大小.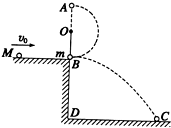 如图所示,O为一水平轴,轴上系一长l=0.6m的细绳,细绳的下端系一质量m=1.0kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触但对平台无压力,平台高h=0.80m,一质量M=2.0kg的小球沿平台自左向右运动到B处与小球m发生正碰,碰后小球m在绳的约束下做圆周运动,经最高点A点,绳上的拉力恰好等于摆球的重力,而M落在水平地面上的C点,其水平位移为s=1.2m,求质量为M的小球与m碰撞前的速度.(取g=10m/s2)
如图所示,O为一水平轴,轴上系一长l=0.6m的细绳,细绳的下端系一质量m=1.0kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触但对平台无压力,平台高h=0.80m,一质量M=2.0kg的小球沿平台自左向右运动到B处与小球m发生正碰,碰后小球m在绳的约束下做圆周运动,经最高点A点,绳上的拉力恰好等于摆球的重力,而M落在水平地面上的C点,其水平位移为s=1.2m,求质量为M的小球与m碰撞前的速度.(取g=10m/s2)