题目内容
 如图所示,四分之一圆环轨道半径为R=0.2m,竖直固定放置在水平地面上,B点为顶点,恰好在圆心O的正上方.一质量为1kg的小球在外力的作用下从最低点A由静止运动到B点,此时撤去外力,小球落地点距O点0.4m,此过程中外力做功为6J.(圆环轨道横截面半径忽略不计,小球可视为质点,g=10m/s2)试求:
如图所示,四分之一圆环轨道半径为R=0.2m,竖直固定放置在水平地面上,B点为顶点,恰好在圆心O的正上方.一质量为1kg的小球在外力的作用下从最低点A由静止运动到B点,此时撤去外力,小球落地点距O点0.4m,此过程中外力做功为6J.(圆环轨道横截面半径忽略不计,小球可视为质点,g=10m/s2)试求:(1)小球到达B点时的速度大小;
(2)小球在B点时对轨道的压力的大小和方向;
(3)小球从A到B过程中,因为摩擦产生的热量Q.
分析:(1)小球从B点开始做平抛运动,由平抛运动基本规律即可求解B点速度;
(2)在B点,设管对球的作用力为N,根据牛顿第二定律列式即可求解;
(3)小球从A到B的过程中,根据动能定理即可求解摩擦力做的功,产生的热量等于克服摩擦力做的功.
(2)在B点,设管对球的作用力为N,根据牛顿第二定律列式即可求解;
(3)小球从A到B的过程中,根据动能定理即可求解摩擦力做的功,产生的热量等于克服摩擦力做的功.
解答:解:(1)小球从B点开始做平抛运动,由平抛运动基本规律得:
x=v0t
R=
gt2
解得:v0=2m/s
(2)在B点,设管对球的作用力为N,根据牛顿第二定律得:
mg+N=m
带入数据解得:N=10N,方向竖直向下,
根据牛顿第三定律可知,小球对轨道的压力大小为10N,方向竖直向上;
(3)小球从A到B的过程中,根据动能定理得:
W+Wf-mgR=
mv02
解得:
Wf=-2J
所以,小球从A到B过程中,因为摩擦产生的热量Q=2J.
答:(1)小球到达B点时的速度大小为2m/s;
(2)小球在B点时对轨道的压力的大小为10N,方向竖直向上;
(3)小球从A到B过程中,因为摩擦产生的热量为2J.
x=v0t
R=
| 1 |
| 2 |
解得:v0=2m/s
(2)在B点,设管对球的作用力为N,根据牛顿第二定律得:
mg+N=m
| v2 |
| R |
带入数据解得:N=10N,方向竖直向下,
根据牛顿第三定律可知,小球对轨道的压力大小为10N,方向竖直向上;
(3)小球从A到B的过程中,根据动能定理得:
W+Wf-mgR=
| 1 |
| 2 |
解得:
Wf=-2J
所以,小球从A到B过程中,因为摩擦产生的热量Q=2J.
答:(1)小球到达B点时的速度大小为2m/s;
(2)小球在B点时对轨道的压力的大小为10N,方向竖直向上;
(3)小球从A到B过程中,因为摩擦产生的热量为2J.
点评:本题主要考查了牛顿第二定律、平抛运动基本公式及动能定理的直接应用,知道产生的热量等于克服摩擦力做的功,难度适中.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图所示的光滑轨道固定在竖直平面内,AB是竖直直杆,BEC是半径为R的半圆,CD是半径为
如图所示的光滑轨道固定在竖直平面内,AB是竖直直杆,BEC是半径为R的半圆,CD是半径为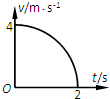 如图所示为某运动物体的v-t图象,该曲线恰好是圆心在坐标原点的四分之一圆,则物体所做的是
如图所示为某运动物体的v-t图象,该曲线恰好是圆心在坐标原点的四分之一圆,则物体所做的是

