题目内容
某人划船,在静水中划行速度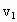 =1.8m/s,若他在水速
=1.8m/s,若他在水速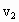 =3m/s的河中匀速划行,则:
=3m/s的河中匀速划行,则:
(1)他怎样划行才能使他在最短时间内到达对岸?
(2)若要使船的实际轨迹最短,他应怎样划行?
答案:略
解析:
解析:
|
(1) 当船头朝与河岸垂直的方向划行时,过河时间最短;(2)当船头朝与上游的夹角为53°方向划行时,实际航程最短.船参与了自身划行和随水漂流两个运动,  、 、 为分速度,船的实际运动速度v为合速度,设河宽为D,船头朝与上游河岸成 为分速度,船的实际运动速度v为合速度,设河宽为D,船头朝与上游河岸成 角方向航行.如图所示.则自身划行的分运动 角方向航行.如图所示.则自身划行的分运动 . .
因为  , ,
所以  . .
当  =90°时,t有最小值.即船的航向应朝垂直河岸 =90°时,t有最小值.即船的航向应朝垂直河岸 和 和 的矢量和,从上图可知:当v⊥ 的矢量和,从上图可知:当v⊥ 时,实际轨迹最短.此时 时,实际轨迹最短.此时
sin θ= / / =1.8/3=0.6 =1.8/3=0.6
∴θ =37°, 与上游夹角为90°-θ=90°-37°=53°. 与上游夹角为90°-θ=90°-37°=53°.
将船在静水中的速度分解为平行于河岸和垂直于河岸两个分量,则过河速度为  ,在水流方向,船的实际速度为 ,在水流方向,船的实际速度为 ,如图所示. ,如图所示.
显然,过河时间只与河宽和船在垂直河岸方向上的分速度有关,当  =90°时,t最小.船对岸的位置则与水速和船速在沿岸方向的分速度有关.当 =90°时,t最小.船对岸的位置则与水速和船速在沿岸方向的分速度有关.当 时,船正达正对岸,当 时,船正达正对岸,当 ,船被冲向游靠岸,当 ,船被冲向游靠岸,当 时船驶向对岸的上游某处靠岸. 时船驶向对岸的上游某处靠岸.
本题由于  ,故船只能在对岸靠下游处靠岸,绝不能横渡过河,不能认为船在横渡过河时时间最短.可见,船速随船相对岸的位置变化而变化. ,故船只能在对岸靠下游处靠岸,绝不能横渡过河,不能认为船在横渡过河时时间最短.可见,船速随船相对岸的位置变化而变化. |

练习册系列答案
相关题目
某人划船渡河,河宽为d,船在静水中划行速度大小为 ,船头方向与河岸间夹角为θ(
,船头方向与河岸间夹角为θ( ),水流动速度大小为
),水流动速度大小为 ,如图所示,则( )
,如图所示,则( )
A.渡河所需的时间为 |
B.渡河所需的时间为 |
| C.若水流的速度突然增大,则渡河所需的时间变长 |
| D.若水流的速度突然增大,则渡河所需的时间变短 |


 某人划船渡河,河宽为d,船在静水中划行速度大小为v1,船头方向与河岸间夹角为θ(θ<90°),水流动速度大小为v2,如图所示,则( )
某人划船渡河,河宽为d,船在静水中划行速度大小为v1,船头方向与河岸间夹角为θ(θ<90°),水流动速度大小为v2,如图所示,则( )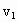 =1.8m/s,若他在水速
=1.8m/s,若他在水速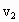 =3m/s的河中匀速划行,则:
=3m/s的河中匀速划行,则:

