题目内容
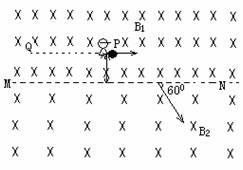
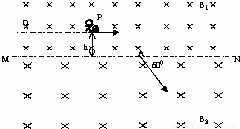
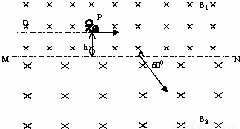
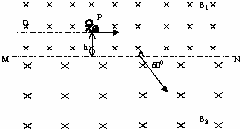如图是计算机模拟出的一种宇宙空间的情境，在此宇宙空间存在这样一个远离其他空间的区域，以MN为界，上部分匀强磁场的磁感强度为B1，下部分的匀强磁场的磁感强度为B2，B1=2B2=2B0，方向相同，且磁场区域足够大．在距离界线为h的P点有一宇航员处于静止状态，宇航员以平行于界线的速度抛出一质量为m、带电量-q的小球，发现球在界线处速度方向与界线成60°角，进入下部分磁场．然后当宇航员沿与界线平行的直线匀速到达目标Q点时，刚好又接住球而静止，求（1）PQ间距离是多大？
（2）宇航员质量是多少？
分析：（1）小球在两个磁场均做匀速圆周运动，由洛仑兹力充当向心力及圆周运动的性质，可求得粒子运动的关径及周期；由粒子运动的对称性可求得PQ间的距离；
（2）由粒子的运动过程可求得宇航员运动的速度；由动量守恒可求得宇航员的质量．
（2）由粒子的运动过程可求得宇航员运动的速度；由动量守恒可求得宇航员的质量．
解答：
解：
（1）画出小球在磁场B1中运动的轨迹如图所示，可知
R1-h=R1cos60°，R1=2h
由qvB=
和B1=2B2
可知R2=2R1=4h
由qv(2B0)=
得v=
根据运动的对称性，PQ的距离为
l=2（R2sin60°-R1sin60°）=2
h；
（2）粒子由P运动到Q的时间t=
+
=
+
=
宇航员匀速运动的速度大小为V=
=
由动量守恒定律得MV-mv=0
可求得宇航员的质量M=
答：（1）PQ间的距离为2
h；（2）宇航员的质量为
．
解：（1）画出小球在磁场B1中运动的轨迹如图所示，可知
R1-h=R1cos60°，R1=2h
由qvB=
| mv2 |
| R |
可知R2=2R1=4h
由qv(2B0)=
| mv2 |
| R1 |
得v=
| 4qB0h |
| m |
根据运动的对称性，PQ的距离为
l=2（R2sin60°-R1sin60°）=2
| 3 |
（2）粒子由P运动到Q的时间t=
| T1 |
| 3 |
| 2T2 |
| 3 |
| 1 |
| 3 |
| 2πm |
| q(2B0) |
| 2 |
| 3 |
| 2πm |
| qB0 |
| 5πm |
| 3qB0 |
宇航员匀速运动的速度大小为V=
| l |
| t |
6
| ||
| 5πm |
由动量守恒定律得MV-mv=0
可求得宇航员的质量M=
| 10πm | ||
3
|
答：（1）PQ间的距离为2
| 3 |
| 10πm | ||
3
|
点评：在解决带电粒子在磁场中的运动时，要“定圆心、求半径”，利用好几何关系进行求解．
练习册系列答案
相关题目
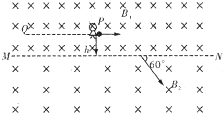如图是计算机模拟出的一种宇宙空间的情境，在此宇宙空间存在这样一个远离其他空间的区域，以MN为界，上部分匀强磁场的磁感应强度为B1，下部分匀强磁场的磁感应强度为B2，B1=2B2=2B0，方向相同，且磁场区域足够大．在距离界线为h的P点有一宇航员处于静止状态，宇航员以平行于界线的速度抛出一质量为m、带电量为-q的小球，发现球在界线处速度方向与界线成60°角进人下部分磁场．然后当宇航员沿与界线平行的直线匀速到达目标Q点时，刚好又接住球而静止，求：
