题目内容
如图所示，水平地面上放置一个质量为m的物体，在与水平方向成θ角、斜向右上方的拉力F的作用下沿水平地面运动。物体与地面间的动摩擦因数为μ，重力加速度为g。求：
（1）若物体在拉力F的作用下能始终沿水平面向右运动，拉力F的大小范围；
（2）已知m＝10 kg、μ＝0．5，g＝10m/s2，若物体以恒定加速度a＝5m/s2向右做匀加速直线运动，维持这一加速度的拉力F的最小值。
要使物体运动时不离开水平面，应有：Fsinθ≤mg -----------------①（2分）
要使物体能向右运动，应有：Fcosθ≥m（mg－Fsinθ）-----------②（1分）
联立①②式得：
≤F≤
（1分）
（2）根据牛顿第二定律得：Fcosθ－m（mg－Fsinθ）＝ma-------------③（2分）
解得：F＝
（2分）
上式变形F＝
，其中a＝sin－1
----------④（2分）
当sin（θ＋a）＝1时F有最小值
解得：Fmin＝
代入相关数值解得：Fmin =40
N （1分）
练习册系列答案
相关题目
（2008?汝城县模拟）如图所示，水平地面上的木块在拉力F的作用下，向右做匀速直线运动，则F与物体受到的地面对它的摩擦力的合力方向为（ ）
（2011?东莞模拟）如图所示，水平地面上的物体A在斜向上的拉力F的作用下，向右做匀速直线运动，则关于下列物体受力情况的说法中正确的是（ ）
如图所示，水平地面上竖直地固定着一个光滑的圆环，一个质量为m的小球套在环上，圆环最高点有一小孔，细线一端被人牵着，另一端穿过小孔与小球相连，使球静止于A处，此时细线与竖直成θ角，重力加速度为g，则不正确的说法是（ ）
如图所示，水平地面上有一辆小车，车上固定一个竖直光滑绝缘管，管的底部有一质量m1=0.2g、电荷量q=8×10-5C的带正电小球，小球的直径比管的内径略小．在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1=15T的匀强磁场，MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场，现让小车始终保持vx=2m/s的速度匀速向右运动，以带电小球刚经过磁场的边界PQ为计时的起点，测得小球在管内运动的这段时间为t=1s，g取10/s2，不计空气阻力．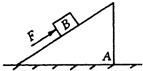 
如图所示，水平地面上有一斜面体A，在A上放一物体B．现对物体B施加一个沿斜面向上且从零逐渐增大的力F，若A、B始终与地面保持相对静止，则（ ）