题目内容
 如图所示,倾角为θ=30°的足够长的固定斜面上,在底端0处固定一垂直斜面的档板,斜面上OM段光滑,M点及以上均粗糙.质量为m的物块A在M点恰好能静止,有一质量为2m的光滑小物块B以初速度v0=
如图所示,倾角为θ=30°的足够长的固定斜面上,在底端0处固定一垂直斜面的档板,斜面上OM段光滑,M点及以上均粗糙.质量为m的物块A在M点恰好能静止,有一质量为2m的光滑小物块B以初速度v0=| 2gL |
(1)A、B第一次碰撞后紧靠在一起的初速度vAB;
(2)物块A在M点上方时,离M点的最大距离s;
(3)系统由于摩擦和碰撞所产生的总内能E.
分析:(1)根据动能定理求出B与A碰撞前的速度,再根据动量守恒定律求出A、B第一次碰撞后紧靠在一起的初速度.
(2)A、B在MO之间运动过程机械能守恒,故A、B返回M点时速度仍为vAB,且来到M 点后由于A受到摩擦力作用,造成AB分离.对A运用动能定理,求出离M点的最大距离.
(3))物块A、B最终紧靠一起在OM间作往复运动,由能的转化和守恒定律求出产生的总内能.
(2)A、B在MO之间运动过程机械能守恒,故A、B返回M点时速度仍为vAB,且来到M 点后由于A受到摩擦力作用,造成AB分离.对A运用动能定理,求出离M点的最大距离.
(3))物块A、B最终紧靠一起在OM间作往复运动,由能的转化和守恒定律求出产生的总内能.
解答:解:(1)小物块B从N点运动到M点由动能定理,有:
2mgLsinθ=
×2m
-
×2m
解得:vB=
,vB为B即将与A碰撞时的速度.
A、B的碰撞过程动量守恒,有:2mvB=(2m+m)vAB
解得vAB=
(2)A、B在MO之间运动过程机械能守恒,故A、B返回M点时速度仍为vAB,且来到M 点后由于A受到摩擦力作用,造成AB分离.
对A自M点往上运动运用动能定理,有:-fs-mgssinθ=0-
m
其中摩擦力f=mgsinθ
解得:s=
(3)物块A、B最终紧靠一起在OM间作往复运动,由能的转化和守恒定律有:E=
×2m
+2mgLsinθ
解得:E=3mgL
答:(1)A、B第一次碰撞后紧靠在一起的初速度vAB=
.
(2)物块A在M点上方时,离M点的最大距离s=
.
(3)系统由于摩擦和碰撞所产生的总内能E=3mgL.
2mgLsinθ=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 0 |
解得:vB=
| 3gl |
A、B的碰撞过程动量守恒,有:2mvB=(2m+m)vAB
解得vAB=
| 2 |
| 3 |
| 3gL |
(2)A、B在MO之间运动过程机械能守恒,故A、B返回M点时速度仍为vAB,且来到M 点后由于A受到摩擦力作用,造成AB分离.
对A自M点往上运动运用动能定理,有:-fs-mgssinθ=0-
| 1 |
| 2 |
| v | 2 AB |
其中摩擦力f=mgsinθ
解得:s=
| gL |
| 15 |
(3)物块A、B最终紧靠一起在OM间作往复运动,由能的转化和守恒定律有:E=
| 1 |
| 2 |
| v | 2 0 |
解得:E=3mgL
答:(1)A、B第一次碰撞后紧靠在一起的初速度vAB=
| 2 |
| 3 |
| 3gL |
(2)物块A在M点上方时,离M点的最大距离s=
| gL |
| 15 |
(3)系统由于摩擦和碰撞所产生的总内能E=3mgL.
点评:本题综合考查了动能定理、动量守恒定律、机械能守恒定律和能量守恒定律,综合性强,对学生能力要求高,关键是理清运动过程,确定出最终的运动状态,运用合适的规律进行求解.

练习册系列答案
相关题目
 如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问:
如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问: 如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8. 如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( )
如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( ) (2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )
(2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )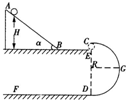 如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的
如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的