题目内容
一个竖直放置的半径为R的光滑绝缘环，置于水平方向的匀强电场中，电场强度大小为E．有一质量为m，电量为正q的空心小球套在环上，如图所示．当小球由静止开始从环的顶端A下滑| 1 | 4 |
分析：由动能定理求出小球到达B点时的速度；
小球做圆周运动，先由动能定理求出小球到达C点时的速度大小，然后由牛顿第二定律列方程，求出小球受到弹力；由牛顿第三定律求出小球对环的压力．
小球做圆周运动，先由动能定理求出小球到达C点时的速度大小，然后由牛顿第二定律列方程，求出小球受到弹力；由牛顿第三定律求出小球对环的压力．
解答：解：从A到B，由动能定理可得：mgR+qER=
mvB2-0，
得：vB=
从A到C，根据动能定理：mg2R=
mvc2-0
得：vc=2
根据牛顿第二定律：N-mg=m
得：N=5mg
由牛顿第三定律，对环的压力的大小为：N′=N=5mg
故答案为：
；5mg．
| 1 |
| 2 |
得：vB=
2gR+
|
从A到C，根据动能定理：mg2R=
| 1 |
| 2 |
得：vc=2
| gR |
根据牛顿第二定律：N-mg=m
| v02 |
| R |
得：N=5mg
由牛顿第三定律，对环的压力的大小为：N′=N=5mg
故答案为：
2gR+
|
点评：由动能定理求出受到，知道弹力与电场力的合力提供向心力是正确解题的关键．
练习册系列答案
相关题目
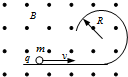如图，一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R的绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B．有一个质量m，带正电量为q的小球在水平轨道上向右运动．恰好能通过最高点，下列正确的是（ ）
如图所示，一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T．有一个质量m=0.10g，带电量为q=+1.6×10-3C的小球在水平轨道上向右运动．若小球恰好能通过最高点，重力加速度g=10m/s2．试求：
（2007?湖北模拟）如图所示，一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T．有一个质量m=0.10g，带电量为q=+1.6×10-3C的小球在水平轨道上向右运动．若小球恰好能通过最高点，则下列说法正确的是（ ）
