题目内容
有一倾角为θ的斜面,其底端固定一挡板M,另有二个木块A、B,它们的质量分别为mA=mB=m,它们与斜面间的动摩擦因数都相同.其中木块A放于斜面上并通过一轻弹簧与挡板M相连,如图所示.开始时,木块A静止在P处,弹簧处于自然伸长状态.木块B在Q点以初速度v向下运动,P、Q间的距离为L.已知木块B在下滑过程中做匀速直线运动,与木块A相撞后立刻一起向下运动,但不粘连.它们到达一个最低点后又向上运动,木块B向上运动恰好能回到Q点.求在此过程中弹簧的最大压缩量.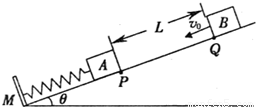
【答案】分析:由题意,B先向下做匀速直线运动,受力平衡,可求得滑动摩擦力与重力的关系;接着B、A碰撞,遵守动量守恒,即可求得碰后共同速度.然后AB压缩弹簧,由系统的机械能守恒列式,可解出两木块被弹簧弹回到P点时的速度.两木块在P点处分开后,木块B上滑到Q点的过程,运用动能定理列式,再联立可解弹簧的最大压缩量.
解答:解:木块B下滑做匀速直线运动,
有 mgsinθ=μmgcosθ ①
B和A相撞前后,总动量守恒,有
mv=2mv1,
∴v1=0.5v ②
设两木块向下压缩弹簧的最大长度为S,两木块被弹簧弹回到P点时的速度为v2,则根据动能定理得
-μ?2mgcosθ?2S=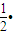 2m
2m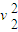 -
-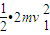 ③
③
两木块在P点处分开后,木块B上滑到Q点的过程:
-(mgsinθ+μmgcosθ)L=0-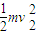 ④
④
由以上四式,可得弹簧的最大压缩量
S=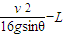 ⑤
⑤
答:在此过程中弹簧的最大压缩量是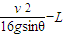 .
.
点评:本题主要考查了动量守恒定律及动能定理的应用,要求同学们能正确选择运动过程,运用相应的规律求解.
解答:解:木块B下滑做匀速直线运动,
有 mgsinθ=μmgcosθ ①
B和A相撞前后,总动量守恒,有
mv=2mv1,
∴v1=0.5v ②
设两木块向下压缩弹簧的最大长度为S,两木块被弹簧弹回到P点时的速度为v2,则根据动能定理得
-μ?2mgcosθ?2S=
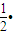 2m
2m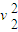 -
-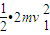 ③
③两木块在P点处分开后,木块B上滑到Q点的过程:
-(mgsinθ+μmgcosθ)L=0-
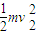 ④
④由以上四式,可得弹簧的最大压缩量
S=
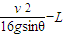 ⑤
⑤答:在此过程中弹簧的最大压缩量是
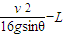 .
.点评:本题主要考查了动量守恒定律及动能定理的应用,要求同学们能正确选择运动过程,运用相应的规律求解.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数
(2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数 如图所示,某一小车中有一倾角为30°的斜面,当小车沿水平方向向左加速运动时,斜面上的物体m与小车始终保持相对静止,求:
如图所示,某一小车中有一倾角为30°的斜面,当小车沿水平方向向左加速运动时,斜面上的物体m与小车始终保持相对静止,求:

