题目内容
如图，在水平面上有两条平行导电导轨MN、PQ，导轨间距离为l，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为m1、m2和R1、R2，两杆与导轨接触良好，与导轨间的动摩擦因数为μ，已知：杆1被外力拖动，以恒定的速度v沿导轨运动；达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2克服摩擦力做功的功率．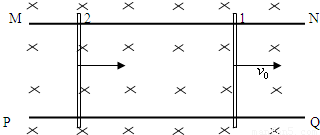
【答案】分析：稳定运动时，即达到平衡状态，根据平衡知识列出等式．
根据电磁感应定律求出感应电流，即求出导体杆2克服摩擦力从而求出功．
解答：解：设杆2的运动速度为v，由于两杆运动时，两杆间和导轨构成的回路中的磁通量发生变化，
产生感应电动势 E=Bl（v-v）①
感应电流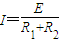
②
杆2作匀速运动，它受到的安培力等于它受到的摩擦力，
BlI=μm2g③
导体杆2克服摩擦力做功的功率 P=μm2gv ④
由①②③④解得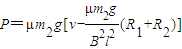
答：此时杆2克服摩擦力做功的功率是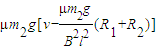
．
点评：本题考查切割产生的感应电动势与电路的结合，在分析中要注意物体运动状态（加速、匀速或平衡）由牛顿第二定律可得出对应的表达式，从而联立求解．
根据电磁感应定律求出感应电流，即求出导体杆2克服摩擦力从而求出功．
解答：解：设杆2的运动速度为v，由于两杆运动时，两杆间和导轨构成的回路中的磁通量发生变化，
产生感应电动势 E=Bl（v-v）①
感应电流
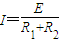②杆2作匀速运动，它受到的安培力等于它受到的摩擦力，
BlI=μm2g③
导体杆2克服摩擦力做功的功率 P=μm2gv ④
由①②③④解得
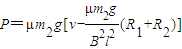
答：此时杆2克服摩擦力做功的功率是
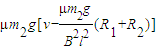．点评：本题考查切割产生的感应电动势与电路的结合，在分析中要注意物体运动状态（加速、匀速或平衡）由牛顿第二定律可得出对应的表达式，从而联立求解．
练习册系列答案
相关题目
如图，在水平面上有两条平行导电导轨MN、PQ，导轨间距离为l，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为m1、m2和R1、R2，两杆与导轨接触良好，与导轨间的动摩擦因数都为μ，已知：杆1被外力拖动，以恒定的速度v0沿导轨运动，达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2的动量大小．
、
和
、
，两杆与导轨接触良好，与导轨间的动摩擦因数都为
，已知：杆1被外力拖动，以恒定的速度
沿导轨运动，达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2的动量大小。
，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为
和
，两杆与导轨接触良好，与导轨间的动摩擦因数为
，已知：杆1被外力拖动，以恒定的速度
沿导轨运动；达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2克服摩擦力做功的功率。
，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为
和
,两杆与导轨接触良好，与导轨间的动摩擦因数为
，已知：杆1被外力拖动，以恒定的速度
沿导轨运动；达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2克服摩擦力做功的功率。