题目内容
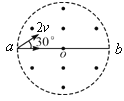
【题目】如图所示，在x轴上方存在匀强磁场，磁感应强度大小为B，方向垂直于纸面向外；在x轴下方存在匀强电场，电场强度大小为E，方向与xoy平面平行，且与x轴成
角。一质量为m、电荷量为
的粒子以速度
从坐标原点O沿与x轴鱼方向成角射出，一段时间后进入电场，不计粒子重力。求：
粒子做匀速圆周运动的半径R和周期T；
粒子从O点出发后，第3次到达x轴所经历的时间t。
【答案】
；
【解析】
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，求解周期及半径；分析清楚粒子在电场中的运动过程，应用牛顿第二定律、运动学公式求出粒子在各运动过程的运动时间，然后求出粒子总的运动时间。
带电粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，有
又有：
解得：
，
由题可知，粒子第1次到达x轴时，转过的角度为
，所需时间
为
粒子进入电场后，先做匀减速运动，直到速度减小为0，然后沿原路返回做匀加速运动，到达x轴时速度大小仍为
，设粒子在电场中运动的总时间为
，加速度大小为a，电场强度大小为E，有：
解得
粒子离开电场第3次通过x轴时，转过的角度为
，所需时间
为
总时间：
解得：
练习册系列答案
金钥匙试卷系列答案
相关题目
