Question

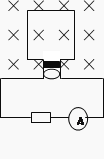
【题目】在科学研究中，可以通过施加适当的电场和磁场来实现对带电粒子运动的控制．如图甲所示，M、N为间距足够大的水平极板，紧靠极板右侧放置竖直的荧光屏PQ，在MN间加上如图乙所示的匀强电场和匀强磁场，电场方向竖直向下，磁场方向垂直于纸面向里，图中E0、B0、k均为已知量．t=0时刻，比荷 =k的正粒子以一定的初速度从O点沿水平方向射入极板间，在0～t1（t1= ）时间内粒子恰好沿直线运动，t= 时刻粒子打到荧光屏上．不计粒子的重力，涉及图象中时间间隔时取0.8= ，1.4= ，求：

（1）在t2= 时刻粒子的运动速度v；
（2）在t3= 时刻粒子偏离O点的竖直距离y；
（3）水平极板的长度L．

Answer 1

【答案】
（1）

解：在0～t1时间内，粒子在电磁场中做匀速直线运动，则：qv0B0=qE0

得

在t1～t2时间内，粒子在电场中做类平抛运动，

=v0

则

由tanθ= 得：θ=45° 即v与水平方向成45o角向下

（2）

解：在电场中做类平抛运动向下偏移：

在t2～t3时间内，粒子在磁场中做匀速圆周运动，运动周期

在磁场中运动时间 ，即圆周运动的圆心角为 α=45°，此时速度恰好沿水平方向．

磁场中：由 得

偏离的竖直距离

（3）

解：在t3时刻进入电场时以初速度 做类平抛运动，

再次进入磁场时，

由tabθ= 得 θ′=45° 即v′与水平方向成45o角向下．

由 得

综上可得：长度 =

【解析】带电粒子在交变的电场和磁场中运动情况比较复杂，既要考虑受力同时还要分析速度方向，分段计算，走一步算一步是本题的关键：（1）在该时间段里，粒子先做匀速直线运动后做类平抛运动，末速度是水平速度和竖直速度的矢量和．（2）在第一问的基础上，求出了末速度大小和方向，向下偏移的距离y1也能求出．紧接着粒子只受洛仑兹力，粒子做匀速圆周运动．由于时间风好是周期的18，所以粒子又转过45°，速度方向又变为水平．由几何关系能求出圆周运动向下偏移的距离y2 ， 两者之和是t3时刻的竖直位移y．（3）同理，在以后的两个时间段里粒子相继做类平抛运动和匀速圆周运动，求出每一时间段的水平位移，那么总的板长就是这几段水平位移之和．
【考点精析】通过灵活运用向心力和洛伦兹力，掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力；洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功即可以解答此题．