题目内容
7．
如图所示，两根长度均为L的细线下端拴一质量为m的小球，两线间的夹角为α．今使摆球在垂直于线面的平面内做小幅度振动，则其振动周期T=$2π\sqrt{\frac{Lcos\frac{α}{2}}{g}}$．
分析 首先将此双线摆转化为单摆，再利用单摆的周期公式即可求解．
解答 解：此摆可等效为摆长为L$cos\frac{α}{2}$的单摆，据单摆的周期公式得球的周期为：T=$2π\sqrt{\frac{Lcos\frac{α}{2}}{g}}$．
故答案为：$2π\sqrt{\frac{Lcos\frac{α}{2}}{g}}$．
点评 将此双线摆转化为单摆模型是解题的关键，注意摆线长为线长与球半径之后．
练习册系列答案
相关题目
18．一物体做直线运动，其v-t图象如图所示，从图中可以看出以下说法正确（ ）
| A． | 0～2s内物体的加速度为1.5 m/s2 | |
| B． | 2～4s内物体静止 | |
| C． | 4 s～6s内，物体先做匀减速直线运动，后做匀加速直线运动 | |
| D． | 0＜t＜2 s和6 s＜t＜8 s内加速度的方向与速度方向均相同 |
2．（多选）物理学史的发展曲曲折折，以下说法正确的是（ ）
| A． | 牛顿提出了运动学里的三大定律，还提出了万有引力定律 | |
| B． | 哥白尼提出所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上 | |
| C． | 自然界中任何两个物体都相互吸引，且引力F=G$\frac{{{M_1}{M_2}}}{R^2}$ | |
| D． | 苹果因为熟了才掉在地上的 |
12．
如图所示，竖直平面内放一直角杆AOB，杆的水平部分粗糙，动摩擦因数为0.20，杆的竖直部分光滑，两部分各套有质量分别为2.0kg和1.0kg的小球A和B，A、B间用细绳相连，初始位置OA=1.5m，OB=2.0m，g取10m/s2，则若用水平拉力F1沿杆向右缓慢拉A，使之移动0.5m，该过程中拉力F1做功（ ）
如图所示，竖直平面内放一直角杆AOB，杆的水平部分粗糙，动摩擦因数为0.20，杆的竖直部分光滑，两部分各套有质量分别为2.0kg和1.0kg的小球A和B，A、B间用细绳相连，初始位置OA=1.5m，OB=2.0m，g取10m/s2，则若用水平拉力F1沿杆向右缓慢拉A，使之移动0.5m，该过程中拉力F1做功（ ）| A． | 3.0J | B． | 8.0J | C． | 0 | D． | 5.0J |
16．
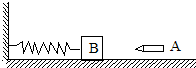如图所示，轻弹簧与木块连接另一端固定在竖直的墙壁上，木块B放于光滑水平面上，弹簧处原长状态，一颗子弹A以水平速度射入木块内（此过程时间非常短），将弹簧压缩到最短，将子弹、木块、弹簧作为系统，则此系统在从子弹接触木块开始到弹簧被压缩至最短的过程中，下列说法中不正确的是（ ）
如图所示，轻弹簧与木块连接另一端固定在竖直的墙壁上，木块B放于光滑水平面上，弹簧处原长状态，一颗子弹A以水平速度射入木块内（此过程时间非常短），将弹簧压缩到最短，将子弹、木块、弹簧作为系统，则此系统在从子弹接触木块开始到弹簧被压缩至最短的过程中，下列说法中不正确的是（ ）| A． | 动量守恒，机械能守恒 | B． | 动量不守恒，机械能不守恒 | ||
| C． | 动量守恒，机械能不守恒 | D． | 动量不守恒，机械能守恒 |
17．下列叙述中的力，属于万有引力的是（ ）
| A． | 马拉车的力 | B． | 钢绳吊起重物的力 | ||
| C． | 太阳与地球之间的吸引力 | D． | 两个异名磁极之问的吸引力 |