Question

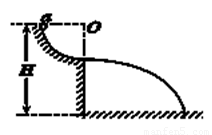
如图所示，有一光滑的T字形支架，在它的竖直杆上套有一个质量为m₁的物体A，用长为l的不可伸长的细绳悬挂在套于水平杆上的小环B下，B的质量为m₂=m₁=m开始时A处于静止状态，系绳处于竖直状态．今用水平恒力F=3mg拉小环B，使A上升至细绳与水平杆成37°，
求：（1）拉力F做的功
（2）末时刻A的速度为大小．

Answer 1

分析：（1）F为恒力，有功的计算公式可求功
（2）由于绳不可伸长，A、B沿绳的分速度相等，分别将A、B的速度进行分解可得两者的速度间的关系，再对A、B连同绳子构成的系统应用动能定理列方程，可求速度的大小．

解答：解：（1）拉力做功：W=FS=FLcos37°=2.4mgL
（2）设A的速度为v_A，B的速度为v_B．由于绳不可伸长，A、B沿绳的分速度相等．分别将A、B、的速度按效果分解得；
v_Bcos37°=v_Asin37°
故vA=

4

3

 v_B
对A、B连同绳子构成的系统应用动能定理：
W-mgL（1-sin37°）=

1 2 mv

2 A

+

1

2

mv

2 B

解得：v_A=

8

5

gL

 
答：（1）拉力F做的功2.4mgL
（2）末时刻A的速度为

8

5

gL

点评：W=FL仅用于恒力做功的计算，对于变力做功不可；本题将A、B的速度沿绳的方向与垂直于绳的分析分解，其中沿绳的方向速度相等是关键．