题目内容
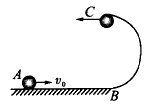
如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以vo=400m/s的水平速度射入木块中,然后一起运动到轨道最高点水平抛出,当圆轨道半径R多大时,平抛的水平距离最大?最大值是多少?(g取10m/s2)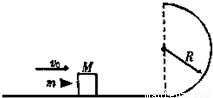
【答案】分析:对子弹和木块应用动量守恒定律求出共同速度,对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面,求出木块到最高点时的速度,由平抛运动的基本规律表示出平抛的水平距离即可求解.
解答:解:对子弹和木块应用动量守恒定律:
mv=(m+M)v1
所以 v1=4m/s
对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面,设木块到最高点时的速度为v2,有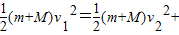 (m+M)g?2R
(m+M)g?2R
所以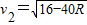
由平抛运动规律有:
2R=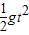
S=v2t
解得:S=4-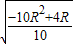
所以,当R=0.2m时水平距离最大
最大值Smax=0.8m.
答:当圆轨道半径R=0.2m时,平抛的水平距离最大,最大值是0.8m.
点评:对于圆周运动,常常是机械能守恒定律或动能定理与牛顿定律的综合.子弹射击木块过程,基本的规律是动量守恒.
解答:解:对子弹和木块应用动量守恒定律:
mv=(m+M)v1
所以 v1=4m/s
对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面,设木块到最高点时的速度为v2,有
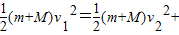 (m+M)g?2R
(m+M)g?2R所以
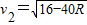
由平抛运动规律有:
2R=
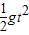
S=v2t
解得:S=4-
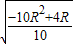
所以,当R=0.2m时水平距离最大
最大值Smax=0.8m.
答:当圆轨道半径R=0.2m时,平抛的水平距离最大,最大值是0.8m.
点评:对于圆周运动,常常是机械能守恒定律或动能定理与牛顿定律的综合.子弹射击木块过程,基本的规律是动量守恒.

练习册系列答案
相关题目
 如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=0.4m,一小球停放在光滑水平轨道上,现给小球一个V0=5m/s的初速度.求:
如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=0.4m,一小球停放在光滑水平轨道上,现给小球一个V0=5m/s的初速度.求: