题目内容
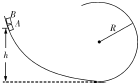
 如图所示,在紧直面内有一个光滑弧形轨道,其末端切线水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接.A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧.两滑块从弧形轨道上的某一高度南静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动.已知圆形轨道的半径R=0.50m,滑块A的质量mA=0.16 kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度,h=0.80m,重力加速度g取1 0m/s2,空气阻力可忽略不计.试求:
如图所示,在紧直面内有一个光滑弧形轨道,其末端切线水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接.A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧.两滑块从弧形轨道上的某一高度南静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动.已知圆形轨道的半径R=0.50m,滑块A的质量mA=0.16 kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度,h=0.80m,重力加速度g取1 0m/s2,空气阻力可忽略不计.试求:(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小;
(2)若滑块A在最低点被弹簧弹开时的速度大小为5.0m/s,求A滑到最高点时对轨道的压力大小.
分析:(1)滑块AB下滑到圆形轨道最低点的过程中,只有重力做功,机械能守恒,由机械能守恒定律列式即可求解;
(2)对于滑块A,从最低点到最高点的过程中,机械能守恒,机械能守恒定律和牛顿运动定律结合求解A滑到最高点时对轨道的压力大小.
(2)对于滑块A,从最低点到最高点的过程中,机械能守恒,机械能守恒定律和牛顿运动定律结合求解A滑到最高点时对轨道的压力大小.
解答:解:(1)设A、B两滑块一起运动到圆形轨道最低点时速度的大小为v0,此过程机械能守恒,则有
(mA+mB)gh=
(mA+mB)
解得 v0=4m/s
(2)设滑块A在最低点被弹簧弹开时的速度大小vA,到达最高点时速度大小为v,对于滑块从最低点到最高点的过程中,根据机械能守恒定律得
mA
=mAg?2R+
mAv2
在最高点,F+mAg=m
联立解得,轨道对小球的弹力为F=0,
则根据牛顿第三定律得知,A滑到最高点时对轨道的压力大小为零.
答:
(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小是4m/s;
(2)A滑到最高点时对轨道的压力大小是零.
(mA+mB)gh=
| 1 |
| 2 |
| v | 2 0 |
解得 v0=4m/s
(2)设滑块A在最低点被弹簧弹开时的速度大小vA,到达最高点时速度大小为v,对于滑块从最低点到最高点的过程中,根据机械能守恒定律得
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
在最高点,F+mAg=m
| v2 |
| R |
联立解得,轨道对小球的弹力为F=0,
则根据牛顿第三定律得知,A滑到最高点时对轨道的压力大小为零.
答:
(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小是4m/s;
(2)A滑到最高点时对轨道的压力大小是零.
点评:本题综合性较强,解决综合问题的重点在于分析物体的运动过程,分过程灵活应用相应的物理规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,光滑水平面AB与光滑半圆形轨道在B点相连,轨道位于竖直面内,其半径为R,一个质量为m的物块静止在水平面上,现向左推物块使其压紧弹簧,然后放手,物块在弹力作用下获得一速度,当它经B点进入半圆轨道,之后向上运动恰能完成半圆周运动到达C点,重力加速度为g.求:
如图所示,光滑水平面AB与光滑半圆形轨道在B点相连,轨道位于竖直面内,其半径为R,一个质量为m的物块静止在水平面上,现向左推物块使其压紧弹簧,然后放手,物块在弹力作用下获得一速度,当它经B点进入半圆轨道,之后向上运动恰能完成半圆周运动到达C点,重力加速度为g.求: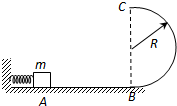 如图所示,光滑水平面AB与位于竖直面内的半圆形轨道在B点平滑连接,半圆形轨道表面粗糙,半径为R.一个质量为m的静止小物块在A点处压紧弹簧,弹簧弹开时小物块在弹力的作用下获得动能向右运动,当它到达B点进入半圆轨道的瞬间,小物块对轨道的压力为其自身重力的7倍,之后沿轨道向上恰能完成圆运动到达C点.求:
如图所示,光滑水平面AB与位于竖直面内的半圆形轨道在B点平滑连接,半圆形轨道表面粗糙,半径为R.一个质量为m的静止小物块在A点处压紧弹簧,弹簧弹开时小物块在弹力的作用下获得动能向右运动,当它到达B点进入半圆轨道的瞬间,小物块对轨道的压力为其自身重力的7倍,之后沿轨道向上恰能完成圆运动到达C点.求: