题目内容
 (2008?南开区模拟)某同学设计了一种测定风力的装置,其原理如图所示.迎风板与一轻弹簧的一端N相接,穿在光滑的金属杆上.弹簧是绝缘材料制成的,其劲度系数k=1300N/m,自然长度L0=0.5m,均匀金属杆用电阻率较大的合金制成,迎风板面积S=0.5m2,工作时总是正对着风吹来的方向.电路中左端导线与金属杆M端相连,右端导线接在N点并可随迎风板在金属杆上无摩擦滑动,且与金属杆接触良好.限流电阻的阻值R=1Ω,电源的电动势E=12V,内阻r=0.5Ω.合上开关,没有风吹时,弹簧处于原长,电压表的示数U1=3.0V;如果某时刻由于风吹使迎风板向左压缩弹簧,电压表的示数变为U2=2.0V,求:
(2008?南开区模拟)某同学设计了一种测定风力的装置,其原理如图所示.迎风板与一轻弹簧的一端N相接,穿在光滑的金属杆上.弹簧是绝缘材料制成的,其劲度系数k=1300N/m,自然长度L0=0.5m,均匀金属杆用电阻率较大的合金制成,迎风板面积S=0.5m2,工作时总是正对着风吹来的方向.电路中左端导线与金属杆M端相连,右端导线接在N点并可随迎风板在金属杆上无摩擦滑动,且与金属杆接触良好.限流电阻的阻值R=1Ω,电源的电动势E=12V,内阻r=0.5Ω.合上开关,没有风吹时,弹簧处于原长,电压表的示数U1=3.0V;如果某时刻由于风吹使迎风板向左压缩弹簧,电压表的示数变为U2=2.0V,求:(1)金属杆单位长度的电阻;
(2)此时作用在迎风板上的风力;
(3)若风(运动的空气)与迎风板作用后速度变为零,已知装置所在处的空气密度为1.3kg/m3,求风速为多大?
分析:(1)定值电阻R与金属杆串联,当无风时,根据电压表示数,应用闭合欧姆定律求出电流,再根据公式R=
求出金属杆接入电路的电阻.
(2)根据有风时电压表示数可用第1题的方法求出金属杆接入电路的电阻,由电阻再求出此时弹簧的长度,根据胡克定律F=Kx,求出风力.
(3)根据动量定理求解风速的大小.
| U |
| I |
(2)根据有风时电压表示数可用第1题的方法求出金属杆接入电路的电阻,由电阻再求出此时弹簧的长度,根据胡克定律F=Kx,求出风力.
(3)根据动量定理求解风速的大小.
解答:解:(1)无风时,金属杆电阻RL
=
RL=0.5Ω
单位长度电阻 r0=
=
=1Ω/m
(2)有风时 U2=
E
R2=0.3Ω
此时弹簧长度L=
=
=0.3m
x=L0-L=0.5-0.3=0.2m
由平衡,此时风力:F=kx=1300×0.2=260N
(3)根据动量定理,有:
F△t=ρs(v△t)v
解得:v=
=
=20m/s
答:(1)金属杆单位长度的电阻为1Ω/m;
(2)此时作用在迎风板上的风力为260N;
(3)风速为20m/s.
| RL |
| RL+R+r |
| 3 |
| 12 |
单位长度电阻 r0=
| RL |
| L |
| 0.5 |
| 0.5 |
(2)有风时 U2=
| R2 |
| R2+R+r |
R2=0.3Ω
此时弹簧长度L=
| R2 |
| r |
| 0.3 |
| 1 |
x=L0-L=0.5-0.3=0.2m
由平衡,此时风力:F=kx=1300×0.2=260N
(3)根据动量定理,有:
F△t=ρs(v△t)v
解得:v=
|
|
答:(1)金属杆单位长度的电阻为1Ω/m;
(2)此时作用在迎风板上的风力为260N;
(3)风速为20m/s.
点评:本题考查电压、电流、电阻的计算,关键是欧姆定律的公式及其变形的应用以及串联电路电压的规律.解决力电综合题,关键寻找力与电的桥梁,本题的桥梁是弹簧的长度.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
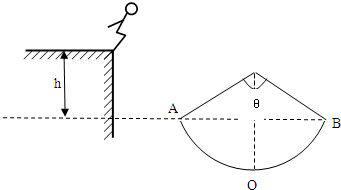 (2008?南开区模拟)如图所示,一玩滚轴溜冰的小孩(可视作质点)质量为m=30kg,他在左侧平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.已知圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8m (计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求:
(2008?南开区模拟)如图所示,一玩滚轴溜冰的小孩(可视作质点)质量为m=30kg,他在左侧平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.已知圆弧半径为R=1.0m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8m (计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)求: (2008?南开区模拟)如图所示,三只完全相同的灯泡a、b、c分别与电阻R、电感L、电容C串联,再将三者并联,接在220V,50Hz的交变电压两端,三只灯泡亮度相同.若将交变电压改为220V,25Hz,则( )
(2008?南开区模拟)如图所示,三只完全相同的灯泡a、b、c分别与电阻R、电感L、电容C串联,再将三者并联,接在220V,50Hz的交变电压两端,三只灯泡亮度相同.若将交变电压改为220V,25Hz,则( ) (2008?南开区模拟)一列简谐横波沿x轴正方向传播,在t1=0时波传播到x轴上的质元B,在它左边的质元A恰好位于负最大位移处,如图所示.在t2=0.6s时,质元A第二次出现在正的最大位移处,则( )
(2008?南开区模拟)一列简谐横波沿x轴正方向传播,在t1=0时波传播到x轴上的质元B,在它左边的质元A恰好位于负最大位移处,如图所示.在t2=0.6s时,质元A第二次出现在正的最大位移处,则( )