题目内容
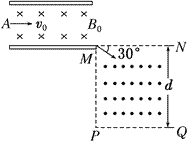
【题目】如图所示，两足够长平行光滑的金属导轨
、
相距为
，导轨平面与水平面夹角为
，导轨电阻不计．磁感应强度为
的匀强磁场垂直导轨平面斜向上，长为
的金属棒
垂直于
、
放置在导轨上，且始终与导轨接触良好，金属棒的质量为
、电阻为
．两金属导轨的上端连接右侧电路，电路中
为一电阻箱，已知灯泡的电阻
，定值电阻
，调节电阻箱使
，重力加速度为
，闭合开关
，现将金属棒由静止释放，求：
（
）金属棒下滑的最大速度
．
（
）当金属棒下滑距离为
时速度恰好达到最大，则金属棒由静止开始下滑
的过程中，整个电路产生的电热．
（
）改变电阻箱
的值，当
为何值时，金属棒达到匀速下滑时
消耗的功率最大．
【答案】（
）
（
）
（
）
【解析】试题分析：闭合开关S，金属棒由静止释放，沿斜面下滑切割磁感线，产生电动势
，相当于电源给电路供电，随着速度的增大电动势增大，当速度达到最大值时，导体棒匀速运动，由受力平衡求出
，由功能关系求出电热，由闭合电路求出R2的功率，由二次函数求出最大值．
（
）当金属棒匀速下滑时速度最大，达到最大时有： 
…①
又
…② 
…③其中
…④
联立①-④式得金属棒下滑的最大速度
…⑤
（
）根据能量转化和守恒得
…⑥
将⑤式代入上式得
．
（
）金属棒匀速下滑时
则得
…⑦
消耗的功率
…⑧．由分流原理得：通过电阻箱
的
…⑨ 联立⑦-⑨式得： 
．
．
当
，即
时， 
消耗的功率最大．
故
消耗的最大功率为
．
练习册系列答案
相关题目
