Question

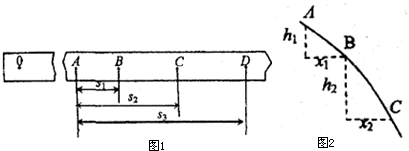
某同学在描绘平抛运动轨迹时，得到的部分轨迹曲线如图所示．在曲线上取A、B、C三个点，测量得到A、B、C三点间竖直距离h₁=10.20cm，h₂=20.20cm，A、B、C三点间水平距离x₁=x₂=12.40cm，g取10m/s²，则物体平抛运动的初速度大小为

1.24

m/s，轨迹上B点的瞬时速度大小为

1.96

m/s．（计算结果保留三位有效数字）

Answer 1

分析：A、B水平距离相等，则时间间隔相等，根据竖直方向上相等时间内的位移之差是一恒量求出相等的时间间隔，结合水平位移和时间间隔求出初速度的大小．
根据竖直方向上某段时间内的平均速度等于中间时刻的瞬时速度，求出B点的竖直分速度，结合平行四边形定则求出B点的瞬时速度．

解答：解：根据h2-h1=gT2得，T=

h2-h1 g

=

0.202-0.102 10

s=0.1s．
则平抛运动的初速度v0=

x

T

=

0.124

0.1

m/s=1.24m/s．
B点竖直方向上分速度vyB=

h1+h2

2T

=

0.102+0.202

0.2

m/s=1.52m/s．
根据平行四边形定则得，vB=

v02+vyB2

=

1.242+1.522

m/s≈1.96m/s．
故答案为：1.24  1.96

点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式和推论灵活求解．