题目内容
如图所示，不计重力的轻杆OP能以O为轴在竖直平面内自由转动，P端悬挂一重物，另用一根轻绳通过定滑轮系在P端．当OP和竖直方向的夹角α缓慢逐渐增大时（0＜α＜π），OP杆的弹力T和绳子的张力F的大小变化是（ ）分析：对P点受力分析，然后根据平衡条件并运用相似三角形法得到OP杆对P的支持力表达式，最后根据牛顿第三定律得到OP杆所受压力表达式再讨论其与角α关系．
解答：解：对点P受力分析，设杆的弹力为N，绳子的拉力为T，如图
根据平衡条件，合力为零，△AOP与图中矢量（力）三角形相似，故有
=
=
解得：N=
G T=
G
由图看出，OP、AO不变，则杆的支持力N不变，AP变大，则绳子拉力T变大．
根据牛顿第三定律，OP杆所受压力等于支持力N，故A正确．
故选A．
根据平衡条件，合力为零，△AOP与图中矢量（力）三角形相似，故有
| N |
| OP |
| T |
| AP |
| G |
| AO |
解得：N=
| OP |
| AO |
| AP |
| AO |
由图看出，OP、AO不变，则杆的支持力N不变，AP变大，则绳子拉力T变大．
根据牛顿第三定律，OP杆所受压力等于支持力N，故A正确．
故选A．
点评：本题是力学的动态分析问题，可以通过解析法求解出表达式后分析，也可以通过作图法分析，可以灵活选择．
练习册系列答案
相关题目
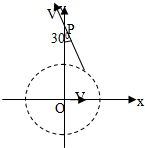（2011?广东模拟）一匀强磁场，磁场方向垂直于xy平面，在xy平面上，磁场分布在以O为中心的一个圆形区域内．一个质量为m，电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x正方向．后来，粒子经过y轴上的P点，此时速度方向与y轴的夹角为30°，P到O的距离为L，如图所示．不计重力的影响．求磁场的磁感应强度B的大小及xy平面上磁场区域的半径R．
如图所示，不计重力的轻杆OP能以O点为圆心在竖直平面内自由转动，P端用轻绳PB挂一重物，另用一根轻绳通过滑轮系住P端．在力F的作用下，当杆OP和竖直方向的夹角α（0＜α＜π）缓慢增大时，力F的大小应（ ）
一匀强磁场，磁场方向垂直于xOy平面，在xOy平面上，磁场分布在以O为圆心的一个圆形区域内．一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x轴正方向．后来，粒子经过y轴上的P点，如图所示．不计重力的影响．粒子经过P点时的速度方向可能是图中箭头表示的（ ）
有一匀强磁场分布在以O为中心的一个圆形区域内，磁场方向垂直于xy平面（磁场未画出）．某时刻起一个质量为m、电荷量为+q的带电粒子，由原点O开始运动，初速为v，方向沿x轴正方向．最终粒子到达y轴上的P点，此时速度方向与y轴的夹角为30°，已知OP的距离为L，如图所示．不计重力的影响．
一匀强磁场，磁场方向垂直于Oxy平面，在Oxy平面上，磁场分布在以O为圆心的一个圆形区域内．一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x轴正方向．后来，粒子经过y轴上的P点，如图所示．不计重力的影响．粒子经过P点时的速度方向可能是图中箭头表示的（ ）| A、箭头a是可能的 | B、箭头b是可能的 | C、箭头c是可能的 | D、箭头d是可能的 |