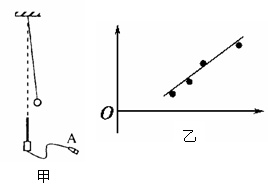
单摆小球的质量为m,摆长为l,摆角为θ,以平衡位置处重力势能为零,则此单摆的振幅为 ,振动的总机械能为 ,摆球通过最低点时的速度为 . 题目和参考答案——青夏教育精英家教网——

题目内容

单摆小球的质量为m,摆长为l,摆角为θ(θ＜10°),以平衡位置处重力势能为零,则此单摆的振幅为_________,振动的总机械能为__________,摆球通过最低点时的速度为__________.

l mgl(1-cosθ)

解析：依据题意可知,单摆的机械能为:E=mgl(1-cosθ)

而单摆的回复力与离开平衡位置的位移的比例系数为:k=.

依据:E=kA²,解得A²===2l²(1-cosθ)

得:A=l

振动的总机械能为:E=mgl(1-cosθ)

设摆球通过最低点的速度为v_m,

据机械能守恒定律得:E=mv²

即v===.

练习册系列答案

钟书金牌新学案作业本系列答案

新同步课课精练系列答案

导学先锋系列答案

零负担试卷系列答案

名牌学校分层周周测系列答案

53金卷3年高考模拟试卷整编系列答案

黄冈海淀全程培优测试卷系列答案

高中同步检测优化卷阶梯训练系列答案

高中同步阶梯训练示范卷系列答案

成功阶梯步步高系列答案

相关题目

（2013?普陀区二模）在“利用单摆测重力加速度”的实验中：
（1）已知单摆小球的质量为m，摆长为l，某地重力加速度为g，当单摆做摆角不超过5°的振动时，通过证明可以得到回复力F=-kx，其中k=

．
（2）某同学尝试用DIS测量周期．如图甲所示，用一个磁性小球代替原先的摆球，在单摆下方放置一个磁传感器，其轴线恰好位于单摆悬挂点正下方．使单摆做小角度摆动，当磁感应强度测量值最大时，磁性小球位于最低点．若测得连续N个磁感应强度最大值之间的时间间隔为t，则单摆周期的测量值为

（地磁场和磁传感器的影响可忽略）．
（3）经理论推导可知，单摆在任意摆角θ时的周期公式可近似为T=T₀（1+

），式中T₀为当摆角θ趋近于0°时的周期．为了用图象法验证该关系式，若某同学在实验中得到了如图乙所示的图线，则图线的斜率为

，纵轴截距为

单摆小球的质量为m,摆长为l,摆角为θ(θ<10°),以平衡位置处重力势能为零,则此单摆的振幅为_________________,振动的总机械能为________________,摆球通过最低点时的速度为________________.

单摆小球的质量为m,摆长为l,摆角为θ(θ<10°),以平衡位置处重力势能为零,则此单摆的振幅为_________________,振动的总机械能为________________,摆球通过最低点时的速度为________________.

在“利用单摆测重力加速度”的实验中：

（1）已知单摆小球的质量为m，摆长为l，某地重力加速度为g，当单摆做摆角不超过5°的振动时，通过证明可以得到回复力F＝－kx，其中k＝_______。

（2）某同学尝试用DIS测量周期。如图甲所示，用一个磁性小球代替原先的摆球，在单摆下方放置一个磁传感器，其轴线恰好位于单摆悬挂点正下方。使单摆做小角度摆动，当磁感应强度测量值最大时，磁性小球位于最低点。若测得连续N个磁感应强度最大值之间的时间间隔为t，则单摆周期的测量值为____________（地磁场和磁传感器的影响可忽略）。

（3）经理论推导可知，单摆在任意摆角θ时的周期公式可近似为T＝T₀（1＋sin²），式中T₀为当摆角θ趋近于0°时的周期。为了用图象法验证该关系式，若某同学在实验中得到了如图乙所示的图线，则图线的斜率为________，纵轴截距为__________。