题目内容
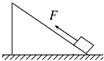 (2013?闵行区一模)如图所示,一物体在平行于斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经时间t力F做功为60J,此后撤去恒力F,物体又经时间t回到出发点,若以地面为零势能点,则当物体回到出发点时的动能为
(2013?闵行区一模)如图所示,一物体在平行于斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经时间t力F做功为60J,此后撤去恒力F,物体又经时间t回到出发点,若以地面为零势能点,则当物体回到出发点时的动能为60
60
J,在撤去恒力F之前,当物体的动能为7J时,物体的机械能为28
28
J.分析:物体向上运动到回到出发点的过程,拉力对物体做功,重力做功零,支持力不做功,根据动能定理,求解当物体回到出发点时的动能.根据题意:物体在拉力作用向上运动时间与撤去恒力F物体回到出发点的时间相等,位移大小相等方向相反,由运动学公式分析得到有拉力与没拉力时物体的加速度关系,根据牛顿第二定律得到拉力与重力的关系,再分析当物体的动能为7J时物体的重力势能的值,求解.
解答:解:设物体回到出发点时的动能为EK1,根据动能定理,WF=△Ek=EK1,EK1=WF=60J
设有拉力与没拉力时物体的加速度大小分别为a1、a2,
根据物体在拉力作用向上运动的位移与撤去拉力后回到出发点的位移大小相等,方向相反
得
a1t2+(a1t)t-
a2t2=0
得到a2=3a1
又由牛顿第二定律得
F-mgsinθ=ma1,mgsinθ=ma2,
得到F=
mgsinθ
设当物体的动能为EK2=7J时,物体重力势能为EP,
(F-mgsinθ)x=EK2
EP=mgsinθx
得到 EP=3EK2,故物体的机械能E=EK2+EP=4EK2=28J
故本题答案是:60;28
设有拉力与没拉力时物体的加速度大小分别为a1、a2,
根据物体在拉力作用向上运动的位移与撤去拉力后回到出发点的位移大小相等,方向相反
得
| 1 |
| 2 |
| 1 |
| 2 |
得到a2=3a1
又由牛顿第二定律得
F-mgsinθ=ma1,mgsinθ=ma2,
得到F=
| 4 |
| 3 |
设当物体的动能为EK2=7J时,物体重力势能为EP,
(F-mgsinθ)x=EK2
EP=mgsinθx
得到 EP=3EK2,故物体的机械能E=EK2+EP=4EK2=28J
故本题答案是:60;28
点评:本题是动能定理与牛顿第二定律、运动学公式的综合应用,第2空难度较大,问题比较隐含,关键是分析前后两个过程的关系.

练习册系列答案
相关题目
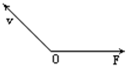 (2013?闵行区一模)如图所示,一个物体在O点以初速度v开始作曲线运动,已知物体只受到恒力F作用,则物体速度大小变化情况是( )
(2013?闵行区一模)如图所示,一个物体在O点以初速度v开始作曲线运动,已知物体只受到恒力F作用,则物体速度大小变化情况是( ) (2013?闵行区一模)如图所示,一列简谐横波沿x轴正方向传播,实线表示t=0时刻的波形,虚线表示t=0.7s时刻的波形.则这列波的( )
(2013?闵行区一模)如图所示,一列简谐横波沿x轴正方向传播,实线表示t=0时刻的波形,虚线表示t=0.7s时刻的波形.则这列波的( )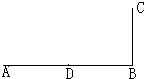 (2013?闵行区一模)如图所示,有一个匀强电场,方向平行于纸面.电场中有A、B、C、D四点,已知AD=DB=BC=d,且AB⊥BC.有一个电量为q的正电荷从A点移动到B点电场力做功为2W,从B点移动到C点克服电场力做功为W.则电场中D点的电势
(2013?闵行区一模)如图所示,有一个匀强电场,方向平行于纸面.电场中有A、B、C、D四点,已知AD=DB=BC=d,且AB⊥BC.有一个电量为q的正电荷从A点移动到B点电场力做功为2W,从B点移动到C点克服电场力做功为W.则电场中D点的电势