题目内容
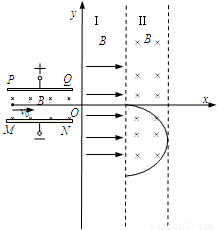
 如图所示,带电平行金属板PQ和MN之间的距离为d;两金属板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B.建立如图所示的坐标系,x轴平行于金属板,且与金属板中心线重合,y轴垂直于金属板.区域I的左边界是y轴,右边界与区域II的左边界重合,且与y轴平行;区域II的左、右边界平行.在区域I和区域II内分别存在匀强磁场,磁感应强度大小均为B,区域I内的磁场垂直于Oxy平面向外,区域II内的磁场垂直于Oxy平面向里.一电子沿着x轴正向以速度v射入平行板之间,在平行板间恰好沿着x轴正向做直线运动,并先后通过区域I和II.已知电子电量为e,质量为m,区域I和区域II沿x轴方向宽度均为
如图所示,带电平行金属板PQ和MN之间的距离为d;两金属板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B.建立如图所示的坐标系,x轴平行于金属板,且与金属板中心线重合,y轴垂直于金属板.区域I的左边界是y轴,右边界与区域II的左边界重合,且与y轴平行;区域II的左、右边界平行.在区域I和区域II内分别存在匀强磁场,磁感应强度大小均为B,区域I内的磁场垂直于Oxy平面向外,区域II内的磁场垂直于Oxy平面向里.一电子沿着x轴正向以速度v射入平行板之间,在平行板间恰好沿着x轴正向做直线运动,并先后通过区域I和II.已知电子电量为e,质量为m,区域I和区域II沿x轴方向宽度均为 .不计电子重力.
.不计电子重力.(1)求两金属板之间电势差U;
(2)求电子从区域II右边界射出时,射出点的纵坐标y;
(3)撤除区域I中的磁场而在其中加上沿x轴正向的匀强电场,使得该电子刚好不能从区域II的右边界飞出.求电子两次经过y轴的时间间隔t.
【答案】分析:(1)粒子做直线运动,电场力等于洛伦兹力,由平衡条件可以求出电势差.
(2)带电粒子在磁场中做匀速直线运动,由牛顿第二定律及数学知识可以求出y轴的坐标.
(3)带电粒子在电场中做加速运动,在磁场中做匀速圆周运动,由牛顿第二定律与匀变速运动规律分析答题.
解答: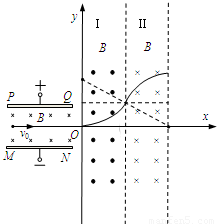 解:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡,
解:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡,
由平衡条件得:eE=evB,①电场强度E=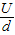 ,②
,②
由①②两式联立解得:U=Bvd;
(2)如右图所示,电子进入区域I做匀速圆周运动,
向上偏转,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m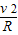 ,③
,③
设电子在区域I中沿着y轴偏转距离为 y,区域I的宽度为b(b=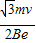 ),
),
由数学知识得:(R-y)2+b2=R2,④
由③④式联立解得:y=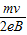 ;
;
因为电子在两个磁场中有相同的偏转量,
故电子从区域II射出点的纵坐标y=2y=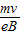 .
.
(3)电子刚好不能从区域II的右边界飞出,
说明电子在区域II中做匀速圆周运动的轨迹恰好与区域II的右边界相切,
圆半径恰好与区域II宽度相同.电子运动轨迹如下图所示.设电子进入区域II时的速度为v,
由牛顿第二定律得:evB=m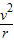 ,⑤
,⑤
由人r=b得:v=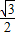 v,
v,
电子通过区域I的过程中,向右做匀变速直线运动,
此过程中平均速度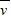 =
=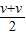 ,
,
电子通过区域I的时间:t1=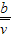 (b为区域I的宽度
(b为区域I的宽度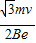 )⑥,
)⑥,
解得:t1=2(2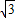 -3)
-3)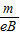 ,
,
电子在区域II中运动了半个圆周,设电子做圆周运动的周期为T,
由牛顿第二定律得:evB=m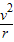 ⑦,v=
⑦,v=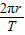 ⑧,
⑧,
电子在区域II中运动的时间:t2=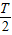 =
=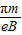 ⑨,
⑨,
由⑦⑧⑨式解得:t2=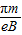 ,
,
电子反向通过区域I的时间仍为t1,电子两次经过y轴的时间间隔:
t=2t1+t2=(8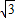 -12+π)
-12+π)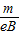 ≈
≈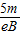 ;
;
答:(1)两金属板之间电势差为Bvd;
(2)电子从区域II右边界射出时,射出点的纵坐标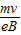 ;
;
(3)电子两次经过y轴的时间间隔为 .
.
点评:本题是一道带电粒子在电场与磁场中运动的综合题,难度较大,根据题意作出粒子的运动轨迹,由牛顿第二定律、运动学公式即可正确解题.
(2)带电粒子在磁场中做匀速直线运动,由牛顿第二定律及数学知识可以求出y轴的坐标.
(3)带电粒子在电场中做加速运动,在磁场中做匀速圆周运动,由牛顿第二定律与匀变速运动规律分析答题.
解答:
 解:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡,
解:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡,由平衡条件得:eE=evB,①电场强度E=
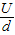 ,②
,②由①②两式联立解得:U=Bvd;
(2)如右图所示,电子进入区域I做匀速圆周运动,
向上偏转,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m
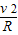 ,③
,③设电子在区域I中沿着y轴偏转距离为 y,区域I的宽度为b(b=
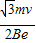 ),
),由数学知识得:(R-y)2+b2=R2,④
由③④式联立解得:y=
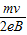 ;
;因为电子在两个磁场中有相同的偏转量,
故电子从区域II射出点的纵坐标y=2y=
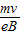 .
.
(3)电子刚好不能从区域II的右边界飞出,
说明电子在区域II中做匀速圆周运动的轨迹恰好与区域II的右边界相切,
圆半径恰好与区域II宽度相同.电子运动轨迹如下图所示.设电子进入区域II时的速度为v,
由牛顿第二定律得:evB=m
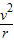 ,⑤
,⑤由人r=b得:v=
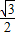 v,
v,电子通过区域I的过程中,向右做匀变速直线运动,
此过程中平均速度
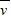 =
=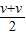 ,
,电子通过区域I的时间:t1=
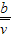 (b为区域I的宽度
(b为区域I的宽度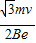 )⑥,
)⑥,解得:t1=2(2
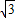 -3)
-3)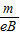 ,
,电子在区域II中运动了半个圆周,设电子做圆周运动的周期为T,
由牛顿第二定律得:evB=m
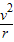 ⑦,v=
⑦,v=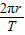 ⑧,
⑧,电子在区域II中运动的时间:t2=
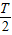 =
=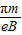 ⑨,
⑨,由⑦⑧⑨式解得:t2=
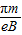 ,
,电子反向通过区域I的时间仍为t1,电子两次经过y轴的时间间隔:
t=2t1+t2=(8
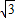 -12+π)
-12+π)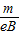 ≈
≈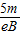 ;
;答:(1)两金属板之间电势差为Bvd;
(2)电子从区域II右边界射出时,射出点的纵坐标
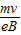 ;
;(3)电子两次经过y轴的时间间隔为
 .
.点评:本题是一道带电粒子在电场与磁场中运动的综合题,难度较大,根据题意作出粒子的运动轨迹,由牛顿第二定律、运动学公式即可正确解题.

练习册系列答案
相关题目
 )如图13所示,两块平行金属板A、B水平放置,板间距离为d,两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态,液滴所带电荷为q。
)如图13所示,两块平行金属板A、B水平放置,板间距离为d,两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态,液滴所带电荷为q。 cm。
cm。
 v0大小;
v0大小; cm。
cm。
