��Ŀ����
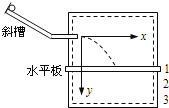
����Ŀ����ͼ����ʾ������ϵ��Ϊk���ᵯ����ֱ���ã��¶˹̶���ˮƽ�����ϣ�һ����Ϊm��С���뵯���϶˸�h���ɾ�ֹ�ͷţ����ڵ����Ϻ���������˶�����͵�Ĺ����У�С����ٶ�v��ʱ��t�ı仯ͼ����ͼ����ʾ������OA��Ϊֱ�ߣ�AB������OA������A������ߣ�BCD��ƽ�������ߣ�����С��ʼ�����λ��Ϊԭ�㣬����ֱ���·�����������Ox�������A��B��C��D�����Ӧ��С�������λ������x������Ӧ�ļ��ٶ�a�Ĵ�С������˵����ȷ���ǣ�������
A.xA=h��aA=0
B.xB=h+ ![]() ��aB=0
��aB=0
C.xC=h+ ![]() ��aC=g
��aC=g
D.xD��h+ ![]() ��aD��g
��aD��g
���𰸡�B,C,D
���������⣺A��OA�������������壬A���������h�����ٶ�Ϊg��A���������⣮
B��B�����ٶ����ĵط�����ʱ�����͵�����ȣ�����Ϊ0�����ٶ�Ҳ��Ϊ0����mg=kx����֪ ![]() ������B������Ϊh+
������B������Ϊh+ ![]() ��B�������⣮
��B�������⣮
C��A��C�������B��Գƣ���A�㵽B����α���Ϊ ![]() ���ɶԳ��Ե���B��C���α���ҲΪ
���ɶԳ��Ե���B��C���α���ҲΪ ![]() ��������C����α���Ϊ
��������C����α���Ϊ ![]() �����Ե��ɵ���F=2mg��F��mg=ma��a=g��x=
�����Ե��ɵ���F=2mg��F��mg=ma��a=g��x= ![]() ������C������Ϊh+
������C������Ϊh+ ![]() ��C�������⣮
��C�������⣮
D������D��ʱ���ٶ�Ϊ0�����Ե���D��ʱ�α���Ҫ����C����α���������D���������h+ ![]() �����ٶ�aD��g��D�������⣮
�����ٶ�aD��g��D�������⣮
�ʴ�Ϊ��BCD
�������֪��OA�������������壬ͼ��A�����������������ĸ߶ȣ���ʱ�ļ��ٶȼ�������������ٶȣ�B�����ٶ����ĵط�����ʱ�����͵�����ȣ�����Ϊ�㣬���ٶ�Ҳ��Ϊ�㣬�ɻ��Լ�������ɵ��α�����C��ʱ�ٶȼ�Ϊ�㣬���ɱ�ѹ������͵㣬���ɵĵ�������Է�������ļ��ٶȣ�

����Ŀ��������Ȼ���ң���������ֱʱ�����ȼ�ΪL�� �� �����¶˹���������ʱ�����ȼ�ΪL0������������ÿ������10g���룬���ɳ������μ�ΪL1��L6 �� �������±�����
|
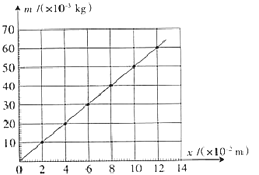
��1��������һ����ֵ��¼���淶����������Ϊ �� �ɱ���֪���ÿ̶ȳߵ���С�ֶ�Ϊ ��
��2��ͼ�Ǹ�ͬѧ���ݱ�����������ͼ������������������������ǵ��ɳ������IJ�ֵ���L����L0������
��3����ͼ��֪���ɺ͵ľ���ϵ��ΪN/m��ͨ��ͼ�ͱ���֪�����̵�����Ϊg�����������λ��Ч���֣��������ٶ�ȡ9.8m/s2����