题目内容
(12分)如图所示,P、Q为水平面内平行放置的光滑金属长直导轨,间距为L1,处在竖直向下、磁感应强度大小为B1的匀强磁场中,一导体杆ef垂直于P、Q放在导轨上,在外力作用下向左做匀速直线运动.质量为m、每边电阻均为r、边长为L2的正方形金属框abcd置于竖直平面内,两顶点a、b通过细导线与导轨相连,磁感应强度大小为B2的匀强磁场垂直金属框向里,金属框恰好处于静止状态,不计其余电阻和细导线对a、b点的作用力.
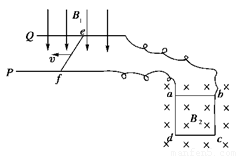
(1)通过ab边的电流Iab是多大?
(2)导体杆ef的运动速度v是多大?
【答案】
(1) 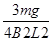 (2)
(2) 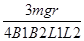
【解析】(1)设通过正方形金属框的总电流为I,ab边的电流为Iab,dc边的电流为Idc,有Iab=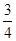 I①
I①
Idc=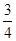 I②
金属框受重力和安培力,处于静止状态,有
I②
金属框受重力和安培力,处于静止状态,有
mg=B2IabL2+B2IdcL2③ 由①~③,解得Iab=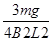 ④
④
(2)由(1)可得I=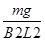 ⑤ 设导体杆切割磁感线产生的电动势为E,有
⑤ 设导体杆切割磁感线产生的电动势为E,有
E=B1L1v⑥设ad、dc、cb三边电阻串联后与ab边电阻并联的总电阻为R,则R=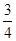 r⑦
r⑦
根据闭合电路欧姆定律,有I=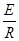 ⑧ 由⑤~⑧,解得v=
⑧ 由⑤~⑧,解得v=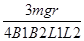 ⑨
⑨
本题考查法拉第电磁感应定律与牛顿运动定律的结合,当导线框静止不动时受力平衡,受到竖直向上的两个安培力的作用,由受力平衡及安培力F=BIl可求得线框电流大小,再由E=BLv可求得导体棒速度

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 (2013?惠州三模)如图所示的轨道由半径为R的1/4光滑圆弧轨道AB、竖直台阶BC、足够长的光滑水平直轨道CD组成.小车的质量为M,紧靠台阶BC且上水平表面与B点等高.一质量为m的可视为质点的滑块自圆弧顶端A点由静止下滑,滑过圆弧的最低点B之后滑到小车上.已知M=4m,小车的上表面的右侧固定一根轻弹簧,弹簧的自由端在Q点,小车的上表面左端点P与Q点之间是粗糙的,滑块与PQ之间表面的动摩擦因数为μ,Q点右侧表面是光滑的.求:
(2013?惠州三模)如图所示的轨道由半径为R的1/4光滑圆弧轨道AB、竖直台阶BC、足够长的光滑水平直轨道CD组成.小车的质量为M,紧靠台阶BC且上水平表面与B点等高.一质量为m的可视为质点的滑块自圆弧顶端A点由静止下滑,滑过圆弧的最低点B之后滑到小车上.已知M=4m,小车的上表面的右侧固定一根轻弹簧,弹簧的自由端在Q点,小车的上表面左端点P与Q点之间是粗糙的,滑块与PQ之间表面的动摩擦因数为μ,Q点右侧表面是光滑的.求: 如图所示,虚线MN左侧是水平正交的匀强电场和磁场,电场水平向右,磁场垂直于纸面向里,磁感应强度为B;MN右侧有竖直方向的匀强电场(图中竖线,未标方向),电场中有一固定点电荷Q.一质量为m,电荷量为q的点电荷,从MN左侧的场区沿与电场线成θ角斜向上的匀速直线运动,穿过MN上的A点进入右侧场区,恰好绕Q在竖直面内做半径为r的匀速圆周运动,并穿过MN上的P点进入左侧场区.已知各电场之间无相互影响,当地重力加速度为g,静电力常量为k.
如图所示,虚线MN左侧是水平正交的匀强电场和磁场,电场水平向右,磁场垂直于纸面向里,磁感应强度为B;MN右侧有竖直方向的匀强电场(图中竖线,未标方向),电场中有一固定点电荷Q.一质量为m,电荷量为q的点电荷,从MN左侧的场区沿与电场线成θ角斜向上的匀速直线运动,穿过MN上的A点进入右侧场区,恰好绕Q在竖直面内做半径为r的匀速圆周运动,并穿过MN上的P点进入左侧场区.已知各电场之间无相互影响,当地重力加速度为g,静电力常量为k.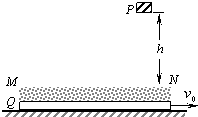 (2005?福建模拟)如图所示,P为位于某一高度处的质量为m的物块,Q为位于水平地面上的质量为M的特殊平板,
(2005?福建模拟)如图所示,P为位于某一高度处的质量为m的物块,Q为位于水平地面上的质量为M的特殊平板,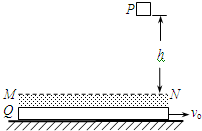 如图所示,P为质量为m=1kg的物块,Q为位于水平地面上的质量为M=4kg的特殊平板,平板与地面间的动摩因数μ=0.02.在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN.P刚从距高h=5m处由静止开始自由落下时,板Q向右运动的速度为vo=4m/s.当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触.在水平方向上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计.( 取g=10m/s2,以下计算结果均保留两位有效数字)求:
如图所示,P为质量为m=1kg的物块,Q为位于水平地面上的质量为M=4kg的特殊平板,平板与地面间的动摩因数μ=0.02.在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN.P刚从距高h=5m处由静止开始自由落下时,板Q向右运动的速度为vo=4m/s.当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触.在水平方向上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计.( 取g=10m/s2,以下计算结果均保留两位有效数字)求: